DifferenceQuotient
DifferenceQuotient[f,{x,h}]
差分係数![]() を与える.
を与える.
DifferenceQuotient[f,{x,n,h}]
複数の差分係数をステップ h で与える.
DifferenceQuotient[f,{x1,n1,h1},{x2,n2,h2},…]
x1,x2,…についての偏差分係数を計算する.
詳細とオプション

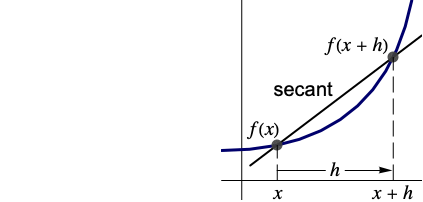
- DifferenceQuotientは,曲線上の近接する2つの点を繋いだ割線の傾きを与える.
- DifferenceQuotient[f,{x,n,h}]は DifferenceDelta[f,{x,n,h}]/
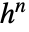 に等しい.
に等しい. - DifferenceQuotient[f,…,Assumptions->assum]は,差分係数の計算過程で仮定 assum を使う.
例題
すべて開くすべて閉じるスコープ (16)
基本的な用法 (4)
DifferenceQuotientはリストに縫い込まれる:
一変量差分係数 (8)
定数のDifferenceQuotientは0である:
多項式関数のDifferenceQuotientは多項式関数である:
整数ステップのPolyGammaの差分係数は有理関数である:
HarmonicNumberとZetaについても同様である:
ステップ h のFactorialPowerは a のマッチするステップ h について単純な差分係数を持つ:
多変量差分係数 (4)
多変量多項式関数のDifferenceQuotientは多項式関数である:
変数の部分集合に依存する多変量関数のDifferenceQuotientは0である:
一変量関数の積についてのDifferenceQuotient:
アプリケーション (10)
第一原理からの導関数 (3)
Dを使って導関数を計算する:
近似導関数 (3)
DifferenceQuotientを使ってある点で導関数を近似する:
DifferenceQuotientによって与えられる近似:
DifferenceQuotientを使ってある点で偏導関数を近似する:
微分方程式 (3)
DSolveValueを使って微分方程式を解く:
RSolveValueを使って微分方程式を解く:
DSolveValueを使って微分方程式を解く:
RSolveValueを使って微分方程式を解く:
DSolveValueを使って微分方程式を解く:
RSolveValueを使って微分方程式を解く:
補外 (1)
Richardson補外法は母数 h に依存する数列 a[h]の収束率を向上させる一連の加速法である.Richardson補外法を使い,DifferenceQuotientの収束を以下で定義される数列 a[x,h]を使って関数 f[x]の導関数に加速させる:
DifferenceQuotientで与えられる近似:
特性と関係 (6)
DifferenceQuotientは,曲線上の近接する2点を結んだ割線の傾きを与える:
DifferenceQuotientのLimitは導関数Dである:
複数の差分係数の反復されたLimitは混合偏微分を与える:
DifferenceQuotientは,![]() のときにDifferenceDeltaと関連している:
のときにDifferenceDeltaと関連している:
DifferenceQuotientは,![]() のときにDiscreteShiftと関連している:
のときにDiscreteShiftと関連している:
DifferenceQuotientは線形演算子である:
テキスト
Wolfram Research (2016), DifferenceQuotient, Wolfram言語関数, https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
CMS
Wolfram Language. 2016. "DifferenceQuotient." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
APA
Wolfram Language. (2016). DifferenceQuotient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferenceQuotient.html