DifferenceQuotient
DifferenceQuotient[f,{x,h}]
给出差商 ![]() .
.
DifferenceQuotient[f,{x,n,h}]
给出 h 步的多重差商.
DifferenceQuotient[f,{x1,n1,h1},{x2,n2,h2},…]
计算 x1,x2,… 的偏差商.
更多信息和选项

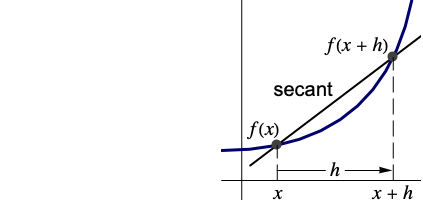
- DifferenceQuotient 给出一条曲线上两个相邻点之间的割线的斜率.
- DifferenceQuotient[f,{x,n,h}] 等价于 DifferenceDelta[f,{x,n,h}]/
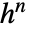 .
. - DifferenceQuotient[f,…,Assumptions->assum] 在计算差商的过程中使用假设 assum.
范例
打开所有单元关闭所有单元范围 (16)
基本用途 (4)
单变量差商 (8)
常数的差商 DifferenceQuotient 为 0:
多项式函数的差商 DifferenceQuotient 为多项式函数:
带有整数步长的 PolyGamma 的差商都是有理函数:
HarmonicNumber 和 Zeta 也类似:
h 步长的 FactorialPower 有一个与 h 步长匹配的 a 的简单差商:
多变量差商 (4)
多变量多项式函数的差商 DifferenceQuotient 是多项式函数:
基于变量子集的多变量函数的差商 DifferenceQuotient 为 0:
单变量函数的乘积的差商 DifferenceQuotient:
应用 (10)
第一性原理的导数 (3)
使用 D 计算导数:
近似导数 (3)
微分方程 (3)
使用 DSolveValue 求解微分方程:
使用 RSolveValue 求解差分方程:
使用 DSolveValue 求解微分方程:
使用 RSolveValue 求解差分方程:
使用 DSolveValue 求解微分方程:
使用 RSolveValue 求解差分方程:
外推法 (1)
理查森外推法是一个应用于数列加速度的方法,可用于提高随参数 h 变化的数列 a[h] 收敛的速率. 使用数列 a[x,h] 和理查森外推法来加速 DifferenceQuotient 收敛于函数 f[x] 的导数,数列定义为:
DifferenceQuotient 给出的近似值:
属性和关系 (6)
DifferenceQuotient 给出连接一条曲线上相近两点的割线的斜率:
差商 DifferenceQuotient 的极限 Limit 是导数 D:
多重差商的迭代极限 Limit 给出混合偏导数:
DifferenceQuotient 与 DifferenceDelta 的关系为 ![]() :
:
DifferenceQuotient 与 DiscreteShift 的关系为 ![]() :
:
DifferenceQuotient 是一个线性运算符:
文本
Wolfram Research (2016),DifferenceQuotient,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
CMS
Wolfram 语言. 2016. "DifferenceQuotient." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DifferenceQuotient.html.
APA
Wolfram 语言. (2016). DifferenceQuotient. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DifferenceQuotient.html 年