Dot 
a.b.c 或 Dot[a,b,c]
给出向量、矩阵和张量的乘积.
更多信息

- a 和 b 是适当维数的列表时,a.b 给出一个明确的结果. 它将 a 中最后一个指标与 b 中第一个指标之间建立约定.
- Dot 的各种应用:
-
{a1,a2}.{b1,b2} 向量的标积 {a1,a2}.{{m11,m12},{m21,m22}}向量和矩阵的乘积 {{m11,m12},{m21,m22}}.{a1,a2}矩阵和向量的乘积 {{m11,m12},{m21,m22}}.{{n11,n12},{n21,n22}}两个矩阵的乘积 - 对两个张量
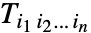 和
和 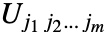 使用 Dot 的结果是张量
使用 Dot 的结果是张量 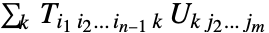 将 Dot 应用到一个
将 Dot 应用到一个 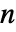 维张量和一个
维张量和一个 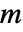 维张量得到一个
维张量得到一个 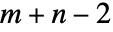 维的张量. »
维的张量. » - 可将 Dot 应用于 SparseArray 和结构化数组对象. 可能的情况下,它将返回与输入相同类型的对象. »
- 对于所有参数,Dot 都是线性的. » 它没有定义向量上的复(厄米特)内积. »
- 当它的参数不是列表或稀疏数组时,Dot 保持不计算. 它具有 Flat 属性.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (28)
向量的点积 (7)
Dot 允许复数输入,但不会取任意一个输入的共轭:
如果想对复数或 Hermitian 内积进行计算,对其中一个输入应用 Conjugate:
用 Norm 验证结果:
计算两个 QuantityArray 向量的标量积:
矩阵-矩阵相乘 (11)
高阶数组 (5)
Dot 适用于任意阶数的数组:
![]() 是完全缩并
是完全缩并 ![]() ,将
,将 ![]() 与
与 ![]() 的最后一层相配,将
的最后一层相配,将 ![]() 与
与 ![]() 的第一层相配:
的第一层相配:
![]() 是不同的缩并
是不同的缩并 ![]() ,将
,将 ![]() 与
与 ![]() 的第一层相配,将
的第一层相配,将 ![]() 与
与 ![]() 的最后一层相配:
的最后一层相配:
两个稀疏数组的 Dot 通常是另一个稀疏数组:
一个稀疏数组与一个普通列表的 Dot 可能是另一个稀疏数组或普通列表:
两个 SymmetrizedArray 对象的乘积通常是另一个对称数组:
应用 (16)
投影和基 (6)
应用 Gram–Schmidt 过程根据以下向量构建正交基:
用 Orthogonalize 确认答案:
Frenet–Serret 系统将每条空间曲线的属性编码到向量基和标量函数中. 考虑以下曲线:
用 FrenetSerretSystem 验证答案:
矩阵和线性算子 (6)
用 OrthogonalMatrixQ 确认:
用 UnitaryMatrixQ 确认:
用 NormalMatrixQ 确认:
正规矩阵包括许多其他类型的矩阵,为正规矩阵的特例. 酉矩阵是正规矩阵:
在量子力学中,具有有限多个状态的系统由单位向量表示,物理量由作用于它们的矩阵表示. 考虑一个自旋 1/2 的粒子,如电子. 它可能处于如下状态:
将 ![]() 与 Dot 一起使用是最快的方法:
与 Dot 一起使用是最快的方法:
具有对称性的矩阵和数组 (4)
属性和关系 (16)
对于每个参数,Dot 都是线性的:
对于实向量 ![]() ,Norm[v] 等于
,Norm[v] 等于 ![]() :
:
对于两个矩阵,![]() 的第
的第 ![]() 和第
和第 ![]() 项是
项是 ![]() 的第
的第 ![]() 行与
行与 ![]() 的第
的第 ![]() 列的点积:
列的点积:
用 MatrixPower 计算重复的矩阵相乘:
对秩为 ![]() 的张量和秩为
的张量和秩为 ![]() 的张量应用 Dot 给出秩为
的张量应用 Dot 给出秩为 ![]() 的张量:
的张量:
Dot 实现了数组的标准内积:
使用 Times 做元素乘法:
可通过 TensorProduct 和 TensorContract 组合使用实现 Dot:
将 Dot 与 Flatten 一起使用以缩并一个数组的多个层级与另一个数组的多个层级:
TensorReduce 可简化含有 Dot 的表达式:
一个行矩阵和列矩阵的 Dot 等于对应向量的 KroneckerProduct:
文本
Wolfram Research (1988),Dot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Dot.html (更新于 2024 年).
CMS
Wolfram 语言. 1988. "Dot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/Dot.html.
APA
Wolfram 语言. (1988). Dot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Dot.html 年
