gives a list of betweenness centralities for the edges in the graph g.
EdgeBetweennessCentrality[{vw,…}]
uses rules vw to specify the graph g.


EdgeBetweennessCentrality
gives a list of betweenness centralities for the edges in the graph g.
EdgeBetweennessCentrality[{vw,…}]
uses rules vw to specify the graph g.
Details
- The edge betweenness centrality of an edge is the number of shortest paths between pairs of vertices that run along it.
- EdgeBetweennessCentrality works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.
Background & Context
- EdgeBetweennessCentrality returns a list of positive machine numbers ("edge betweenness centralities") that approximate particular centrality measures of the edges of a graph. For graphs on one or more edges, edge betweenness centralities lie between
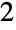 and
and ![2TemplateBox[{{{n, ^, 2}, /, 4}}, Floor] 2TemplateBox[{{{n, ^, 2}, /, 4}}, Floor]](Files/EdgeBetweennessCentrality.en/2.png) inclusive. Edge betweenness centrality is a measure of centrality of an edge in a network based on the number of shortest paths that pass through the given edge. It therefore identifies edges in the network that are crucial for information flows. This measure has found applications in social networks, transportation, biology, and social sciences.
inclusive. Edge betweenness centrality is a measure of centrality of an edge in a network based on the number of shortest paths that pass through the given edge. It therefore identifies edges in the network that are crucial for information flows. This measure has found applications in social networks, transportation, biology, and social sciences. - For a connected graph, let
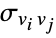 denote the number of shortest paths between vertices
denote the number of shortest paths between vertices 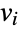 and
and 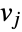 , and let
, and let 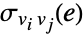 denote the number of shortest paths between
denote the number of shortest paths between 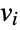 and
and 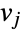 that go through the edge
that go through the edge 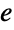 . Then the edge betweenness centrality
. Then the edge betweenness centrality 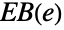 of edge
of edge 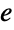 is defined as
is defined as 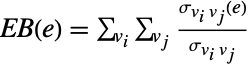 .
. - BetweennessCentrality applies the same betweenness concept to find the vertex-based betweenness centrality.
Examples
open all close allBasic Examples (2)
Scope (7)
EdgeBetweennessCentrality works with undirected graphs:
Use rules to specify the graph:
EdgeBetweennessCentrality works with large graphs:
Applications (5)
Rank the edges of a graph by the number of shortest paths that run along them:
Highlight the edge betweenness centrality for CycleGraph:
A road network linking Chicago suburbs. Find the most central roads, assuming that Chicago residents use the shortest routes to travel:
The two roads that are part of most shortest paths:
A power grid network representing the topology of the Western States Power Grid of the United States. Identify sections of the grid that may carry the most load:
A view of the critical sections:
A metabolic cellular network for Mycobacterium bovis. The frequency of the edge betweenness centrality has a Poisson-like distribution with a very sharp spike:
Properties & Relations (2)
Edge betweenness centralities for an undirected graph are equivalent to centralities for each component:
Computing the centralities for each component yields the same result:
Use EdgeIndex to obtain the centrality of a specific vertex:
Related Guides
Text
Wolfram Research (2012), EdgeBetweennessCentrality, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeBetweennessCentrality.html (updated 2015).
CMS
Wolfram Language. 2012. "EdgeBetweennessCentrality." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EdgeBetweennessCentrality.html.
APA
Wolfram Language. (2012). EdgeBetweennessCentrality. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EdgeBetweennessCentrality.html
BibTeX
@misc{reference.wolfram_2025_edgebetweennesscentrality, author="Wolfram Research", title="{EdgeBetweennessCentrality}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EdgeBetweennessCentrality.html}", note=[Accessed: 24-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_edgebetweennesscentrality, organization={Wolfram Research}, title={EdgeBetweennessCentrality}, year={2015}, url={https://reference.wolfram.com/language/ref/EdgeBetweennessCentrality.html}, note=[Accessed: 24-February-2026]}