ElectricPotentialCondition
ElectricPotentialCondition[pred,vars,pars]
適用場所を示す述語 pred,モデル変数 vars,大域パラメータ pars で,偏微分方程式の電位平面境界条件を表す.
ElectricPotentialCondition[pred,vars,pars,lkey]
pars[lkey]で指定された局所パラメータで電位平面境界条件を表す.
詳細


- ElectricPotentialConditionは,ElectrostaticPDEComponentおよびElectricCurrentPDEComponentのディリクレ(Dirichlet)境界条件を指定する.
- ElectricPotentialConditionは,ElectrostaticPDEComponentとElectricCurrentPDEComponentの境界条件を指定する.
- ElectricPotentialConditionは,一般に,境界における特定の電位を設定するために使われる.一般的な例には,電圧差を加えることによって充電される容量性デバイスが含まれる.
- ElectricPotentialConditionは,従属変数
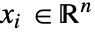 と独立変数
と独立変数 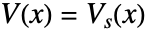 で境界における特定の電位を指定する.
で境界における特定の電位を指定する. - 定常変数 vars は vars={V[x1,…,xn],{x1,…,xn}}である.
- 周波数依存変数 vars は vars={V[x1,…,xn],ω,{x1,…,xn}}である.
- 定常または周波数領域の電位条件ElectricPotentialConditionモデル
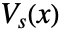 .ただし,
.ただし,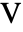 [
[![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricPotentialCondition.ja/6.png) ]は与えられた表面電位である.
]は与えられた表面電位である. - 以下の追加的なモデルパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "ElectricPotential" - 0
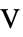 ,表面電位(単位:[
,表面電位(単位:[![TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "V", volts, "Volts"}, QuantityTF]](Files/ElectricPotentialCondition.ja/8.png) ])
]) - モデルパラメータ pars は,ElectrostaticPDEComponentおよびElectricCurrentPDEComponentに対してと同じように指定される.
- 所定の電位条件境界は次の場合に使用できる.
-
分析タイプ 使用可能どうか 周波数応答 可能 定常 可能 - ElectricPotentialConditionを評価するとDirichletConditionになる.
- 境界述語 pred はDirichletConditionにおけるのと同じように指定できる.
- ElectricPotentialConditionが連想 pars で…,keypi…,pivi,…]として指定されるパラメータ
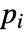 に依存するなら,パラメータ
に依存するなら,パラメータ 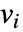 は
は 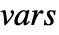 で置換される.
で置換される.
例題
すべて開くすべて閉じるテキスト
Wolfram Research (2024), ElectricPotentialCondition, Wolfram言語関数, https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html (2024年に更新).
CMS
Wolfram Language. 2024. "ElectricPotentialCondition." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html.
APA
Wolfram Language. (2024). ElectricPotentialCondition. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ElectricPotentialCondition.html