WOLFRAM

Wolfram 语言与系统 参考资料中心
Wolfram 语言首页 »

EllipticFilterModel
✖
EllipticFilterModel

✖

设计阶数为 n 的低通椭圆滤波器.

✖

使用截止频率 ωc.

✖
EllipticFilterModel[{"type",spec}]

使用 spec 设计具有指定类型 "type" 的椭圆滤波器.

✖
EllipticFilterModel[{"type",spec},var]

以变量 var 表示模型.

更多信息

  • EllipticFilterModel 以 TransferFunctionModel 的形式返回设计的滤波器.
  • EllipticFilterModel[{n,ω}] 在频率 ω 处返回衰减量为 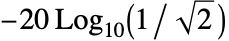(约为 3 dB）的低通滤波器.
  • EllipticFilterModel[n] 使用截止频率1.
  • 滤波器规范 {"type",spec} 可以是以下任何形式之一：
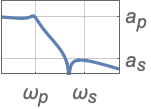
  • {"Lowpass",{ωp,ωs},{ap,as}}使用带通和带阻频率和衰减量的低通滤波器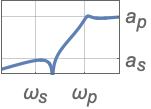
    {"Highpass",{ωs,ωp},{as,ap}}高通滤波器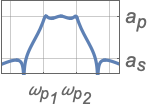
    {"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}}带通滤波器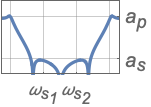
    {"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}}带阻滤波器
  • 频率数值应该以升序给出.
  • 数值 ap 和 as 分别是通带和阻带衰减的绝对值.
  • 给出增益分数 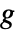，衰减 .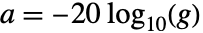

范例

打开所有单元关闭所有单元

基本范例  (2)常见实例总结

处的截止频率的三阶椭圆滤波器模型：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-7pxsg8
Out[1]=1

滤波器的波特图：

In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-4mhlea
Out[2]=2

使用完全指定的低通椭圆滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-hncdle
Out[1]=1

显示离线滤波器特征的滤波器的幅值响应：

In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-n0aucs
Out[2]=2

范围  (8)标准用法实例范围调查

2阶低通滤波器的符号式表示：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-vaen5v
Out[1]=1

提取模型的计算：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-m1h6eu
Out[1]=1

精度为24的模型的计算：

In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-p05e4
Out[2]=2

使用变量 s 创建滤波器模型：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-kvokb4
Out[1]=1

创建截止频率为10的低通滤波器模型：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-kbcoac
Out[1]=1

创建低通椭圆滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-oesfmo
Out[1]=1

创建高通椭圆滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-p84jvh
Out[1]=1

创建带通椭圆滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-u5m4xg
In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-nbsh0v
Out[2]=2

创建带阻椭圆滤波器：

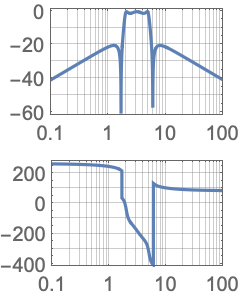
In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-0oe078
In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-bkc32q
Out[2]=2

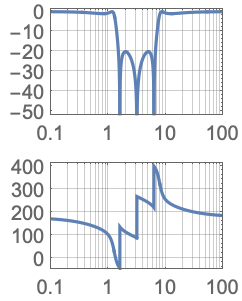
应用  (6)用该函数可以解决的问题范例

创建一个低通椭圆滤波器：

In[11]:=11
✖
https://wolfram.com/xid/08utdckd9mzms3x-e59vk3

滤波一个正弦波信号中的高频噪声：

In[12]:=12
✖
https://wolfram.com/xid/08utdckd9mzms3x-wos954

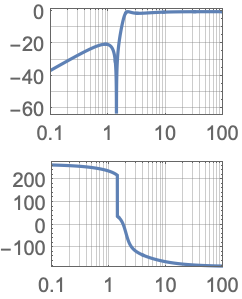
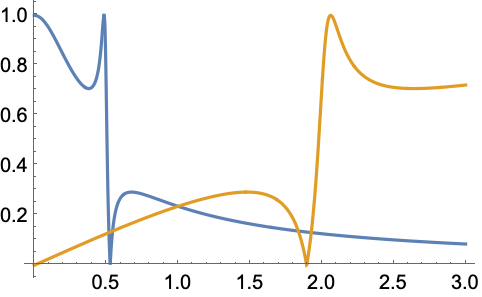
椭圆滤波器把响应移动 Arg[tf[ω ]，其中 ω 是输入正弦波的频率：

In[14]:=14
✖
https://wolfram.com/xid/08utdckd9mzms3x-bu2l3m
Out[14]=14

对相位平移进行校正：

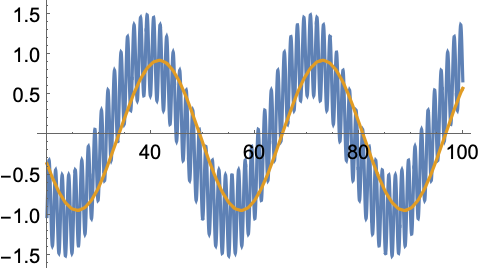
In[17]:=17
✖
https://wolfram.com/xid/08utdckd9mzms3x-kym4bq
Out[18]=18

从低通原型系统创建高通椭圆滤波器：

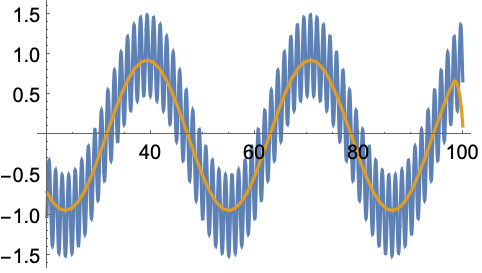
In[7]:=7
✖
https://wolfram.com/xid/08utdckd9mzms3x-relai9

滤波输入的低频正弦波：

In[19]:=19
✖
https://wolfram.com/xid/08utdckd9mzms3x-ztenhq
Out[19]=19

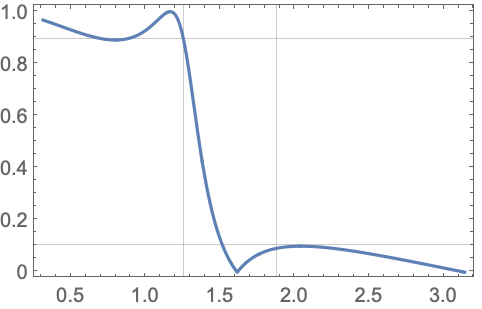
使用满足以下通带和阻带频率和衰减的椭圆近似设计数字低通滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-eg2rp4

假设采样周期为 1 获取等价的模拟频率：

In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-l3l58
Out[2]=2

计算模拟椭圆滤波器传递函数：

In[3]:=3
✖
https://wolfram.com/xid/08utdckd9mzms3x-dg7zm
Out[3]=3

转换成离散时间模型：

In[4]:=4
✖
https://wolfram.com/xid/08utdckd9mzms3x-ecvjhx
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/08utdckd9mzms3x-fld0kc
Out[5]=5

创建离散时间的椭圆 IIR 滤波器的 FIR 近似.

应用低通数字椭圆滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-buj3xd
Out[1]=1

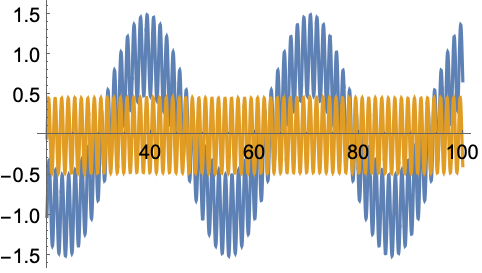
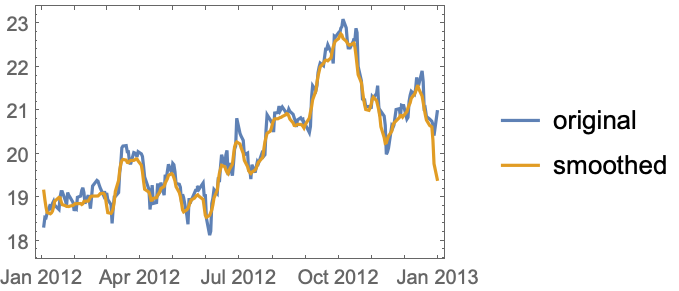
从离散时间椭圆滤波器的脉冲响应获取 FIR 采样想要的数字：

In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-carst7
Out[2]=2

绘制 FIR 滤波器：

In[3]:=3
✖
https://wolfram.com/xid/08utdckd9mzms3x-obd08
Out[3]=3

使用椭圆滤波器的 FIR 近似平滑金融数据：

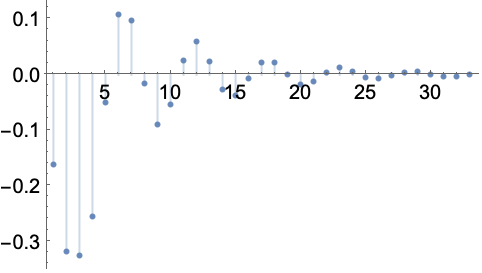
In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-detozt
Out[1]=1

使用低通椭圆滤波器对图像进行滤波：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-cspnd1
Out[1]=1

使用高通椭圆滤波器对图像滤波：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-7ffkuh
Out[1]=1

属性和关系  (3)函数的属性及与其他函数的关联

提取椭圆滤波器的阶数：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-zlcb4j
Out[1]=1

提取椭圆滤波器的极点和零点：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-gnxflg
In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-hltc50
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08utdckd9mzms3x-246wdr
Out[3]=3

把低通滤波器转化为高通滤波器：

In[1]:=1
✖
https://wolfram.com/xid/08utdckd9mzms3x-nwqhwq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08utdckd9mzms3x-cyjc8z
Out[2]=2
Wolfram Research (2012)，EllipticFilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticFilterModel.html.
✖
Wolfram Research (2012)，EllipticFilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticFilterModel.html.

文本

Wolfram Research (2012)，EllipticFilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticFilterModel.html.

✖
Wolfram Research (2012)，EllipticFilterModel，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EllipticFilterModel.html.

CMS

Wolfram 语言. 2012. "EllipticFilterModel." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticFilterModel.html.

✖
Wolfram 语言. 2012. "EllipticFilterModel." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticFilterModel.html.

APA

Wolfram 语言. (2012). EllipticFilterModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EllipticFilterModel.html 年

✖
Wolfram 语言. (2012). EllipticFilterModel. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EllipticFilterModel.html 年

BibTeX

@misc{reference.wolfram_2025_ellipticfiltermodel, author="Wolfram Research", title="{EllipticFilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticFilterModel.html}", note=[Accessed: 04-April-2025 ]}

✖
@misc{reference.wolfram_2025_ellipticfiltermodel, author="Wolfram Research", title="{EllipticFilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticFilterModel.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_ellipticfiltermodel, organization={Wolfram Research}, title={EllipticFilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/EllipticFilterModel.html}, note=[Accessed: 04-April-2025 ]}

✖
@online{reference.wolfram_2025_ellipticfiltermodel, organization={Wolfram Research}, title={EllipticFilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/EllipticFilterModel.html}, note=[Accessed: 04-April-2025 ]}