WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

ButterworthFilterModel
✖
ButterworthFilterModel

✖

creates a lowpass Butterworth filter of order n and cutoff frequency of 1.

✖

uses the cutoff frequency ωc.

✖
ButterworthFilterModel[{"type",spec}]

creates a filter of a given "type" using the specified parameters spec.

✖
ButterworthFilterModel[{"type",spec},var]

expresses the model in terms of the variable var.

Details

  • ButterworthFilterModel returns the filter as a TransferFunctionModel.
  • ButterworthFilterModel[{n,ω}] returns a lowpass filter with attenuation of 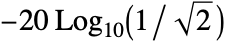(approximately 3 dB) at frequency ω.
  • ButterworthFilterModel[n] uses the cutoff frequency of 1.
  • Lowpass filter specification {"type",spec} can be any of the following:
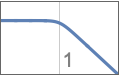
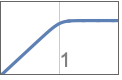
  • {"Lowpass",n}lowpass filter of order n and cutoff frequency 1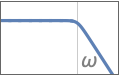
    {"Lowpass",n,ωp}use cutoff frequency ωp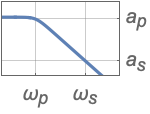
    {"Lowpass",{ωp,ωs},{ap,as}}use full filter specification giving passband and stopband frequencies and attenuations
  • Highpass filter specifications:
  • {"Highpass",n}highpass filter with cutoff frequency 1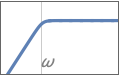
    {"Highpass",n,ωp}use cutoff frequency ωp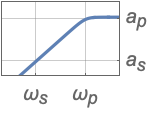
    {"Highpass",{ωs,ωp},{as,ap}}full filter specification
  • Bandpass filter specifications:
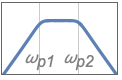
  • {"Bandpass",n,{ωp1,ωp2}}bandpass filter with passband frequencies ωp1 and ωp2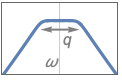
    {"Bandpass",n,{{ω,q}}}use center frequency ω and quality factor q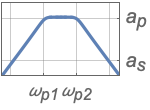
    {"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}}full filter specification
  • Bandstop filter specifications:
  • {"Bandstop",n,{ωp1,ωp2}}bandstop filter with passband frequencies ωp1 and ωp2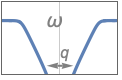
    {"Bandstop",n,{{ω,q}}}use center frequency ω and quality factor q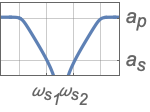
    {"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}}full filter specification
  • Values ap and as are, respectively, absolute values of passband and stopband attenuations.
  • Given a gain fraction 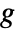, the attenuation is .
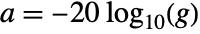  • The quality factor q is defined as 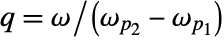, with 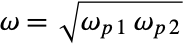being the center frequency of a bandpass or bandstop filter. Higher values of q give narrower filters.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

A third-order Butterworth filter model with cutoff frequency at :

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-7pxsg8
Out[1]=1

Bode plot of the filter:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-4mhlea
Out[2]=2

A lowpass Butterworth filter using the full specification:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-j3twtf
Out[1]=1

Magnitude response of the filter showing the ideal filter characteristics:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-id9gho
Out[2]=2

Scope  (6)Survey of the scope of standard use cases

A symbolic lowpass Butterworth filter of order 3 with a cutoff frequency ω:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-frejvo
Out[1]=1

Use cutoff frequency :

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-kbcoac
Out[1]=1

Same filter using the full specification:

In[4]:=4
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-b5ea69
Out[4]=4

Create a highpass Butterworth filter of order 3 with a cutoff frequency of 10:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-eynflz
Out[1]=1

Same filter using the full specification:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-7af73j
Out[2]=2

Create a "Bandpass" filter with passband frequencies and and attenuation of order 3:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-jiywtz
Out[1]=1

Same filter using center frequency and quality factor specification {{ω,q}}:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-ixovrt
Out[2]=2

Same filter using the full specification:

In[3]:=3
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-druaky
Out[3]=3

Create a bandstop Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-f7kgql
In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-lzrfx3
Out[2]=2

Exact computation of the model:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-m1h6eu
Out[1]=1

Computation of the model with precision 24:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-p05e4
Out[2]=2

Create a filter model using the variable s:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-kvokb4
Out[1]=1

Applications  (6)Sample problems that can be solved with this function

Create a lowpass Butterworth filter:

In[17]:=17
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-3wi1v

Filter out high-frequency noise from a sinusoidal signal:

In[18]:=18
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-ifgc2o

Butterworth filter phase shifts the response by Arg[tf[ω ]], where ω is the frequency of the input sinusoid:

In[20]:=20
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-2jrez2
Out[20]=20

Correct for the phase shift:

In[21]:=21
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-0cddd
Out[22]=22

Create a highpass Butterworth filter from the lowpass prototype:

In[23]:=23
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-n0gy7m

Filter out low-frequency sinusoid from the input:

In[25]:=25
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-ztenhq
Out[25]=25

Design a digital FIR lowpass filter using the Butterworth approximation that satisfies the following passband and stopband frequencies and attenuations:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-u9bcxq

Obtain the equivalent analog frequencies assuming a sampling period of 1:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-l3l58
Out[2]=2

Compute the analog Butterworth transfer function:

In[3]:=3
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-dg7zm
Out[3]=3

Convert to discrete-time model:

In[4]:=4
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-ecvjhx
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-fld0kc
Out[5]=5

Create an FIR approximation of a discrete-time Butterworth IIR filter.

Implement a lowpass digital Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-buj3xd
Out[1]=1

Obtain the desired number of FIR samples from the impulse response of the discrete-time Butterworth filter:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-carst7
Out[2]=2

Plot the FIR filter:

In[3]:=3
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-obd08
Out[3]=3

Smooth financial data using an FIR approximation of a Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-detozt
Out[1]=1

Filter an image using a discrete-time lowpass Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-e9pkl
Out[1]=1

Filter an image using a highpass Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-nmld7q
Out[1]=1

Properties & Relations  (9)Properties of the function, and connections to other functions

Stopband attenuation increases by a factor of per decade as order increases:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-khcsbq
Out[2]=2

Passband width of "Bandpass" filter decreases with increasing quality factor q:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-ejl0fl
Out[1]=1

Phase response of a third-order lowpass Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-fqxb00
Out[1]=1

Compare phase responses for different filter orders:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-b58ugj
Out[2]=2

Phase response of a "Bandpass" filter for several quality factors:

In[3]:=3
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-g3rv0t
Out[3]=3

Extract the order of the Butterworth polynomial:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-zlcb4j
Out[1]=1

The order of the Butterworth polynomial for lowpass and highpass is the same as the specified order:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-zl7hjb
Out[1]=1

The filter order for bandpass and bandstop is twice the given order:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-tocbb5
Out[2]=2

Show the Butterworth polynomial in the denominator of the transfer function:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-j8q3ad
Out[1]=1

Find the poles of a Butterworth filter by solving for the roots of the denominator:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-8mo9vy
In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-bnp6ym
Out[2]=2

Extract poles using TransferFunctionPoles:

In[3]:=3
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-b4cuq
Out[3]=3

Plot poles of the Butterworth filter:

In[4]:=4
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-cbtnsh
Out[4]=4

Implement a lowpass digital Butterworth filter:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-kh9gwp
Out[1]=1

Plot poles of the digital Butterworth filter:

In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-bu0m6
Out[2]=2

Create a highpass filter using a lowpass prototype:

In[1]:=1
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-jsttxk
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08ejj3guu1kjvroxv79ul-cyslq6
Out[2]=2
Wolfram Research (2012), ButterworthFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (updated 2016).
✖
Wolfram Research (2012), ButterworthFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (updated 2016).

Text

Wolfram Research (2012), ButterworthFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (updated 2016).

✖
Wolfram Research (2012), ButterworthFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/ButterworthFilterModel.html (updated 2016).

CMS

Wolfram Language. 2012. "ButterworthFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ButterworthFilterModel.html.

✖
Wolfram Language. 2012. "ButterworthFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ButterworthFilterModel.html.

APA

Wolfram Language. (2012). ButterworthFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ButterworthFilterModel.html

✖
Wolfram Language. (2012). ButterworthFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ButterworthFilterModel.html

BibTeX

@misc{reference.wolfram_2025_butterworthfiltermodel, author="Wolfram Research", title="{ButterworthFilterModel}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ButterworthFilterModel.html}", note=[Accessed: 31-May-2025 ]}

✖
@misc{reference.wolfram_2025_butterworthfiltermodel, author="Wolfram Research", title="{ButterworthFilterModel}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ButterworthFilterModel.html}", note=[Accessed: 31-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_butterworthfiltermodel, organization={Wolfram Research}, title={ButterworthFilterModel}, year={2016}, url={https://reference.wolfram.com/language/ref/ButterworthFilterModel.html}, note=[Accessed: 31-May-2025 ]}

✖
@online{reference.wolfram_2025_butterworthfiltermodel, organization={Wolfram Research}, title={ButterworthFilterModel}, year={2016}, url={https://reference.wolfram.com/language/ref/ButterworthFilterModel.html}, note=[Accessed: 31-May-2025 ]}