EllipticTheta
EllipticTheta[a,u,q]
gives the theta function ![]()
![]() .
.
EllipticTheta[a,q]
gives the theta constant ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
![TemplateBox[{1, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)(-1)^nq^(n(n+1))sin((2 n+1)u) TemplateBox[{1, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)(-1)^nq^(n(n+1))sin((2 n+1)u)](Files/EllipticTheta.en/4.png) .
.![TemplateBox[{2, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)q^(n(n+1))cos((2 n+1)u) TemplateBox[{2, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)q^(n(n+1))cos((2 n+1)u)](Files/EllipticTheta.en/5.png) .
.![TemplateBox[{3, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)q^(n^2)cos(2n u) TemplateBox[{3, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)q^(n^2)cos(2n u)](Files/EllipticTheta.en/6.png) .
.![TemplateBox[{4, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)(-1)^nq^(n^2)cos(2n u) TemplateBox[{4, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)(-1)^nq^(n^2)cos(2n u)](Files/EllipticTheta.en/7.png) .
.- The
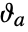 are only defined within the unit q disk,
are only defined within the unit q disk, ![TemplateBox[{q}, Abs]<1 TemplateBox[{q}, Abs]<1](Files/EllipticTheta.en/9.png) ; the unit disk forms a natural boundary of analyticity.
; the unit disk forms a natural boundary of analyticity. - Within the unit q disk,
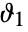 and
and 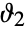 have branch cuts from
have branch cuts from 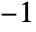 to
to 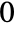 .
. - For certain special arguments, EllipticTheta automatically evaluates to exact values.
- EllipticTheta can be evaluated to arbitrary numerical precision.
- EllipticTheta automatically threads over lists.
- EllipticTheta can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (3)
Scope (20)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
EllipticTheta can be used with Interval and CenteredInterval objects:
Specific Values (3)
EllipticTheta evaluates symbolically for special arguments:
Find the first positive minimum of EllipticTheta[3,x,1/2]:
Visualization (2)
Plot the EllipticTheta function for various parameters:
Function Properties (10)
Real and complex domains of EllipticTheta:
EllipticTheta is a periodic function with respect to ![]() :
:
EllipticTheta threads elementwise over lists:
For example, ![]() has no singularities or discontinuities:
has no singularities or discontinuities:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
![]() is neither non-negative nor non-positive:
is neither non-negative nor non-positive:
![]() is neither convex nor concave:
is neither convex nor concave:
TraditionalForm formatting:
Generalizations & Extensions (1)
EllipticTheta can be applied to a power series:
Applications (11)
Plot theta functions near the unit circle in the complex q plane:
The number of representations of ![]() as a sum of four squares:
as a sum of four squares:
Verify Jacobi's triple product identity through a series expansion:
Conformal map from an ellipse to the unit disk:
Visualize the map:
Green's function for the 1D heat equation with Dirichlet boundary conditions and initial condition ![]() :
:
Plot the time‐dependent temperature distribution:
Form Bloch functions of a one‐dimensional crystal with Gaussian orbitals:
Plot Bloch functions as a function of the quasi‐wave vector:
Electrostatic potential in a NaCl‐like crystal with point-like ions:
Plot the potential in a plane through the crystal:
A concise form of the Poisson summation formula:
An asymptotic approximation for a finite Gaussian sum:
Compare the approximate and exact values for ![]() :
:
Closed form of iterates of the arithmetic‐geometric mean:
Compare the closed form with explicit iterations:
Form any elliptic function with given periods, poles and zeros as a rational function of EllipticTheta:
Form an elliptic function with a single and a double zero and a triple pole:
Properties & Relations (2)
Numerically find a root of a transcendental equation:
Sum can generate elliptic theta functions:
Possible Issues (4)
Machine-precision input is insufficient to give a correct answer:
Use arbitrary-precision arithmetic to obtain the correct result:
The first argument must be an explicit integer between 1 and 4:
EllipticTheta has the attribute NHoldFirst:
Different argument conventions exist for theta functions:
Neat Examples (1)
Visualize a function with a boundary of analyticity:
Text
Wolfram Research (1988), EllipticTheta, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticTheta.html (updated 2022).
CMS
Wolfram Language. 1988. "EllipticTheta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticTheta.html.
APA
Wolfram Language. (1988). EllipticTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticTheta.html