gives the parameter m corresponding to the nome q in an elliptic function.


InverseEllipticNomeQ
gives the parameter m corresponding to the nome q in an elliptic function.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
- InverseEllipticNomeQ[q] yields the unique value of the parameter m which makes EllipticNomeQ[m] equal to q.
- The nome q must always satisfy
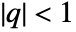 .
. - InverseEllipticNomeQ can be evaluated to arbitrary numerical precision.
- InverseEllipticNomeQ automatically threads over lists.
Examples
open all close allBasic Examples (4)
Scope (26)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix InverseEllipticNomeQ function using MatrixFunction:
Specific Values (4)
Find a value of ![]() for which InverseEllipticNomeQ[x]=0.9:
for which InverseEllipticNomeQ[x]=0.9:
Visualization (2)
Plot the InverseEllipticNomeQ function for various parameters:
Function Properties (10)
Real domain of InverseEllipticNomeQ:
Complex domain of InverseEllipticNomeQ:
InverseEllipticNomeQ threads element-wise over lists:
InverseEllipticNomeQ is an analytic function over its real domain:
In general, it has both singularities and discontinuities:
InverseEllipticNomeQ is nondecreasing over its real domain:
InverseEllipticNomeQ is injective:
InverseEllipticNomeQ is not surjective:
InverseEllipticNomeQ is neither non-negative nor non-positive:
InverseEllipticNomeQ is concave over its real domain:
TraditionalForm formatting:
Differentiation (2)
Series Expansions (2)
Find the Taylor expansion using Series:
Generalizations & Extensions (1)
InverseEllipticNomeQ can be applied to power series:
Applications (4)
Convert between elliptic modulus and nome in elliptic function identities:
Partition function for a one‐atom monatomic gas in a finite container of unit length:
Form partition functions for n bosonic particles:
Calculate and plot mean energies:
InverseEllipticNomeQ is a modular function. Make an ansatz for a modular equation:
Form an overdetermined system of equations and solve it:
This is the modular equation of order 2:
Verify using Series:
Find the modulus corresponding to the elliptic curve, specified by Weierstrass invariants:
Compute the modulus alternatively using InverseEllipticNomeQ:
Properties & Relations (5)
Possible Issues (2)
InverseEllipticNomeQ remains unevaluated outside its domain of analyticity:
InverseEllipticNomeQ is single valued, and EllipticNomeQ is multivalued:
See Also
Tech Notes
Related Guides
Related Links
History
Introduced in 1996 (3.0)
Text
Wolfram Research (1996), InverseEllipticNomeQ, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html.
CMS
Wolfram Language. 1996. "InverseEllipticNomeQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html.
APA
Wolfram Language. (1996). InverseEllipticNomeQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html
BibTeX
@misc{reference.wolfram_2025_inverseellipticnomeq, author="Wolfram Research", title="{InverseEllipticNomeQ}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html}", note=[Accessed: 19-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inverseellipticnomeq, organization={Wolfram Research}, title={InverseEllipticNomeQ}, year={1996}, url={https://reference.wolfram.com/language/ref/InverseEllipticNomeQ.html}, note=[Accessed: 19-January-2026]}