EllipticTheta
EllipticTheta[a,u,q]
シータ(Theta)関数 ![]()
![]() を与える.
を与える.
EllipticTheta[a,q]
シータ定数 ![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学関数である.
-
![TemplateBox[{1, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)(-1)^nq^(n(n+1))sin((2 n+1)u) TemplateBox[{1, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)(-1)^nq^(n(n+1))sin((2 n+1)u)](Files/EllipticTheta.ja/4.png)
-
![TemplateBox[{2, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)q^(n(n+1))cos((2 n+1)u) TemplateBox[{2, u, q}, EllipticTheta]=2q^(1/4)sum_(n=0)^(infty)q^(n(n+1))cos((2 n+1)u)](Files/EllipticTheta.ja/5.png)
-
![TemplateBox[{3, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)q^(n^2)cos(2n u) TemplateBox[{3, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)q^(n^2)cos(2n u)](Files/EllipticTheta.ja/6.png)
-
![TemplateBox[{4, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)(-1)^nq^(n^2)cos(2n u) TemplateBox[{4, u, q}, EllipticTheta]=1+2sum_(n=1)^(infty)(-1)^nq^(n^2)cos(2n u)](Files/EllipticTheta.ja/7.png)
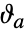 は単位 q の円板,
は単位 q の円板,![TemplateBox[{q}, Abs]<1 TemplateBox[{q}, Abs]<1](Files/EllipticTheta.ja/9.png) ,の中でしか定義されない.単位円板は解析性における自然の境界になる.
,の中でしか定義されない.単位円板は解析性における自然の境界になる.- 単位 q の円板内では,
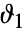 と
と 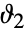 は
は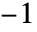 から
から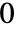 で分枝切断線を持つ.
で分枝切断線を持つ. - 特別な引数の場合,EllipticThetaは,自動的に厳密値を計算する.
- EllipticThetaは任意の数値精度で評価できる.
- EllipticThetaは自動的にリストに縫い込まれる.
- EllipticThetaはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
例題
すべて開くすべて閉じるスコープ (20)
数値評価 (5)
EllipticThetaはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる:
特定の値 (3)
可視化 (2)
関数の特性 (10)
EllipticThetaの実領域と複素領域:
EllipticThetaは ![]() について周期関数である:
について周期関数である:
EllipticThetaは要素単位でリストに縫い込まれる:
TraditionalFormによる表示:
一般化と拡張 (1)
EllipticThetaはベキ級数に適用できる:
アプリケーション (11)
ディリクレ(Dirichlet)境界条件と初期条件 ![]() を持つ一次元の熱伝導方程式のためのグリーン(Green)の関数:
を持つ一次元の熱伝導方程式のためのグリーン(Green)の関数:
ガウス(Gauss)の軌道で一次元結晶のブロッホ(Bloch)関数を形成する:
指定の周期,極,零点を持った任意の楕円関数をEllipticThetaの有理関数として形成する:
特性と関係 (2)
考えられる問題 (4)
EllipticThetaは属性NHoldFirstを持つ:
テキスト
Wolfram Research (1988), EllipticTheta, Wolfram言語関数, https://reference.wolfram.com/language/ref/EllipticTheta.html (2022年に更新).
CMS
Wolfram Language. 1988. "EllipticTheta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticTheta.html.
APA
Wolfram Language. (1988). EllipticTheta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticTheta.html