EstimatorGains

EstimatorGains[ssm,{p1,p2,…,pn}]

推定器の極が pi になるようなStateSpaceModel ssm の推定器ゲイン行列を与える．

EstimatorGains[{ssm,{out1,…}},…]

使用するための計測された出力 outi を指定する．

詳細とオプション

  • EstimatorGainsは観測器ゲインあるいは観測器極配置としても知られている．
  • 状態空間モデル ssm はStateSpaceModel[{a,b,c,d}]で与えられる．ただし，a，b，c，d は連続時間系あるいは離散時間系のいずれかにおける状態，入力，出力，伝送の各行列を表す．
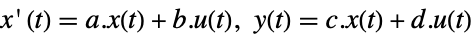
  • 連続時間系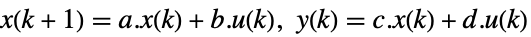
    離散時間系
  • ssm が可観測である場合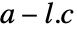， の固有値は{p1,p2,…,pn}である．ただし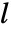， は計算された推定器ゲイン行列である．
  • ディスクリプタ系StateSpaceModel[{a,b,c,d,e}]の場合，指定できる極の数は e の階数と系の可観測性によって決定される． »
  • EstimatorGainsは，AffineStateSpaceModelおよびNonlinearStateSpaceModelによって指定される非線形系もまた許容する．
  • 非線形系については，状態変数および入力変数の操作値が考慮され，ゲインは近似テイラー線形化に基づいて計算される．
  • EstimatorGains[{ssm,{out1,…}},…]はEstimatorGains[ssm1,…]と等価である．ただし，ssm1SystemsModelExtract[ssm,All,{out1,…}]である．
  • 観測器の力学は以下で与えられる．
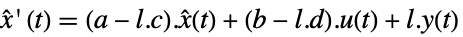
  • 連続時間系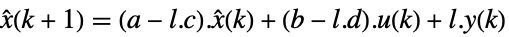
    離散時間系
  • 正方非特異行列 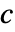の場合，状態ベクトルは x=TemplateBox[{c}, Inverse].(y-d.u)で計算できる．
  • EstimatorGainsは，次の設定で与えられるMethodオプションを取る．
  • Automatic自動メソッド選択
    "Ackermann"Ackermannメソッド
    "KNVD"Kautsky–Nichols–Van Doorenメソッド
  • 推定器ゲインは双対系の状態フィードバックゲインとして計算される．

例題

すべて開くすべて閉じる

例  (3)

連続時間系の推定器ゲインを計算する：

離散時間系：

第2出力のみが測定されている二出力系の推定器ゲイン：

スコープ  (6)

単一入力単一出力(SISO)の系のゲインの集合：

解を証明する：

二出力系の観測器ゲイン行列：

測定値が指定されている三出力系の推定器ゲイン行列：

多項式の根として指定された極を使って推定器ゲインを計算する：

推定器ゲインを記号的に決定する：

AffineStateSpaceModelについてのゲインを計算する：

推定器を組み立てる：

推定器の極は所望の位置にある：

オプション  (6)

Method  (6)

状態より出力が多い系では，AutomaticはLinearSolveを使ってゲインを求める：

デフォルトで厳密値の系にはAckermannメソッドが使われる：

記号値の場合もAckermann法が使われる：

数値を持つ系の場合，Automaticでは"KNVD"法が使われる：

厳密ではない多出力状態空間モデルと，所望の推定器の極の位置：

第1入力に対する可観測性行列の条件数を求める：

第2入力に対する可観測性行列の条件数を求める：

デフォルトで，条件数が最小の出力が選ばれる：

第1出力から推定についてのゲインを求める：

KNVDメソッドは使用可能なすべての出力を使って状態を推定する：

アプリケーション  (2)

連続時間系の観測器を構築する：

ランダムな初期条件から入力がSin[t]の系のシミュレーションを行う：

各状態とその推定を比べる：

ゼロ入力のサンプルデータの系の観測器を構築する：

初期状態{1,–0.75,0.5}で初期観測器状態が{0,0,0}の場合の実際の状態と推定される状態を計算する：

観測器で得た状態追跡を調べる：

特性と関係  (7)

誤差の力学：

StateOutputEstimatorは状態と出力の両方を推定する観測器を組み立てる：

離散時間系の予測推定器の力学：

推定器ゲインは双対系の状態フィードバックゲインの共役転置である：

逆もまた真なり：

可観測の特異ではないディスクリプタ系では，推定器のすべての極を置くことができる：

可観測の特異系については，MatrixRank[e]極のみを置くことができる：

遅い部分系のみが可観測である衝撃系：

遅い部分系の推定器の極のみを置くことができる：

考えられる問題  (4)

KNVDメソッドは出力数が状態数より少ない厳密な系は扱わない：

数値評価を行う：

KNVDメソッドは極の多重度が出力数を上回るケースは扱えない：

Ackermannメソッドを使う：

KNVDメソッドはコンピュータシステムによっては異なるゲイン集合を与えることがある：

観測器の固有値は同じである：

系は可観測でなければならない：

これは可観測ではない：

Wolfram Research (2010), EstimatorGains, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatorGains.html （2014年に更新）.

テキスト

Wolfram Research (2010), EstimatorGains, Wolfram言語関数， https://reference.wolfram.com/language/ref/EstimatorGains.html （2014年に更新）.

CMS

Wolfram Language. 2010. "EstimatorGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/EstimatorGains.html.

APA

Wolfram Language. (2010). EstimatorGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EstimatorGains.html

BibTeX

@misc{reference.wolfram_2024_estimatorgains, author="Wolfram Research", title="{EstimatorGains}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatorGains.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_estimatorgains, organization={Wolfram Research}, title={EstimatorGains}, year={2014}, url={https://reference.wolfram.com/language/ref/EstimatorGains.html}, note=[Accessed: 17-November-2024 ]}