WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

StateFeedbackGains
✖
StateFeedbackGains

✖
StateFeedbackGains[sspec,{p1,…,pn}]

gives the state feedback gains for the system specification sspec to place its closed-loop poles at pi.

✖
StateFeedbackGains[…,"prop"]

gives the value of the property "prop".

Details and Options

  • StateFeedbackGains is also known as pole placement or eigenvalue placement.
  • StateFeedbackGains is used to compute a regulating controller or tracking controller.
  • StateFeedbackGains works by modifying the closed-loop system poles to be at positions pi.
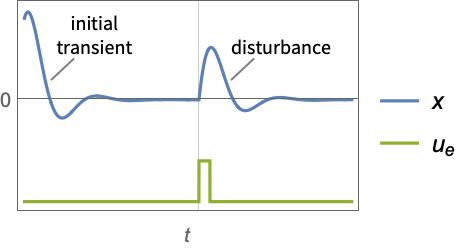
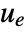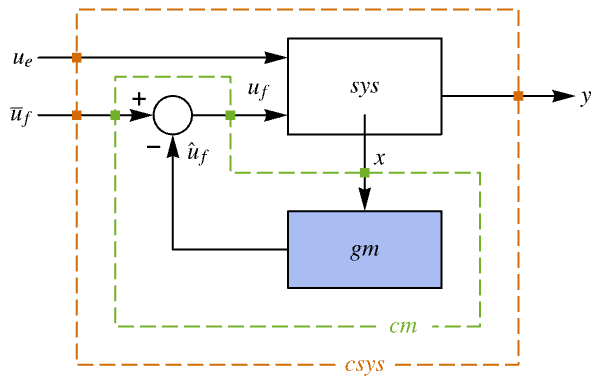
  • A regulating controller aims to maintain the system at an equilibrium state despite disturbances pushing it away. Typical examples include maintaining an inverted pendulum in its upright position or maintaining an aircraft in level flight.
  • The regulating controller is given by a control law of the form 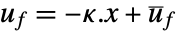, where 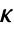is the computed gain matrix.
  • The number of poles n to place is given by SystemsModelOrder of the system sys.
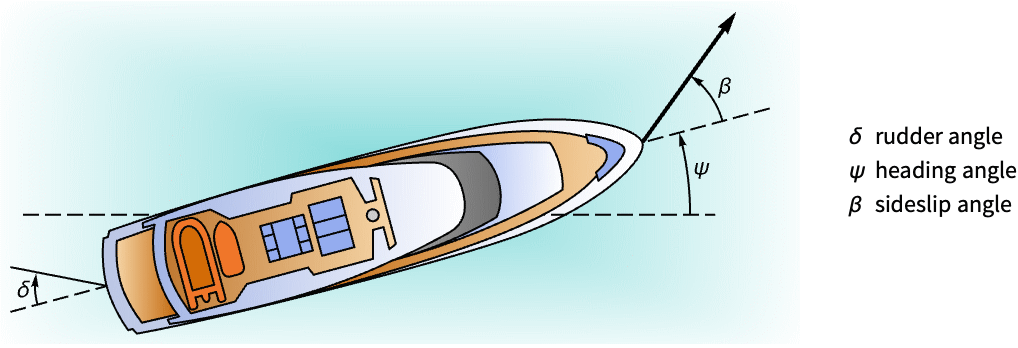
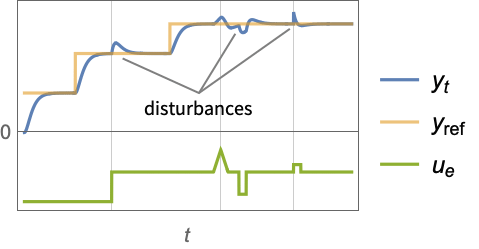
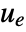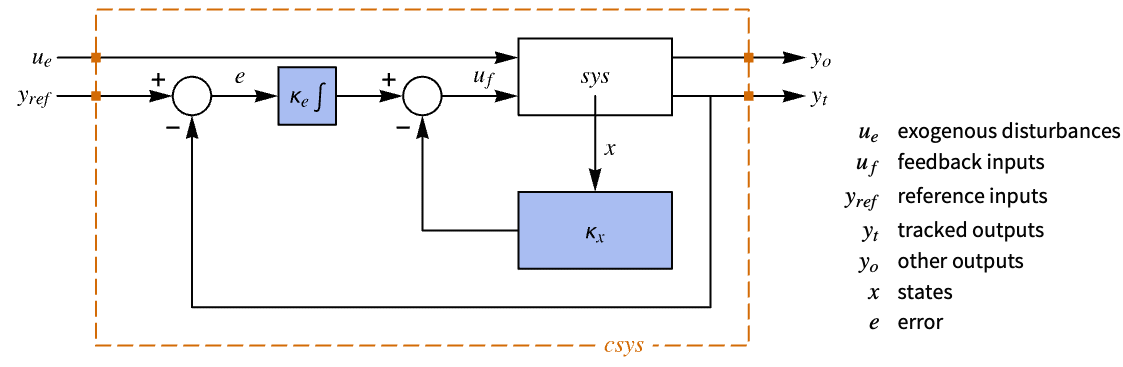
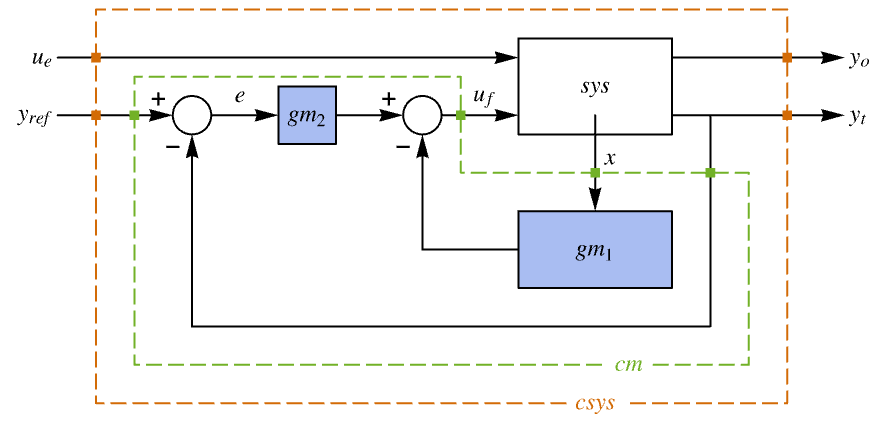
  • A tracking controller aims to track a reference signal despite disturbances interfering with it. Typical examples include a cruise control system for a car or path tracking for a robot.
  • The tracking controller is given by a control law of the form 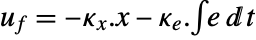, where 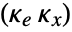is the computed gain matrix for the augmented system that includes the system sys as well as the dynamics for .
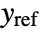  • The number of poles n to place is given by 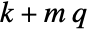, where 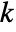is given by SystemsModelOrder of sys, 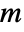the order of yref and 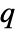the number of signals yref.
  • Pole placement works for linear systems as specified by StateSpaceModel:
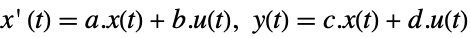
  • continuous-time system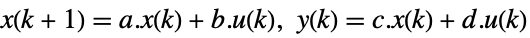
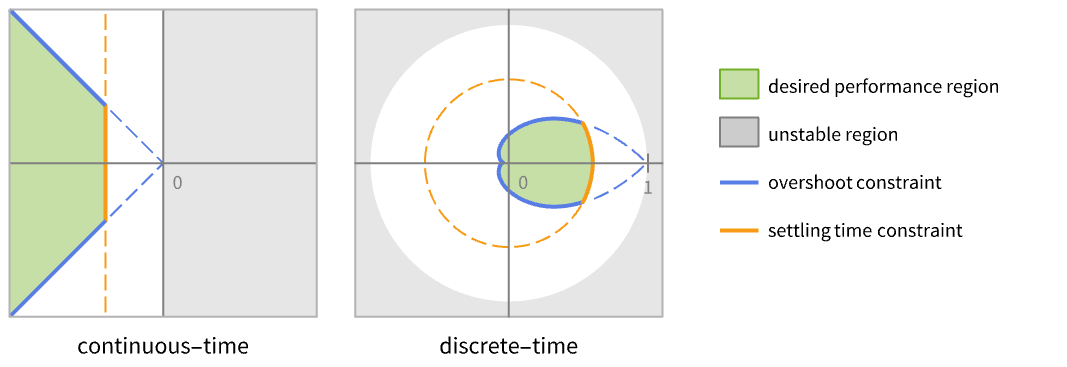
    discrete-time system
  • The performance of the resulting closed-loop system csys is primarily determined by the location of the poles pi.
  • Typically there are performance constraints such as settling time and quality constraints such as overshoot. These correspond to certain regions that are desirable pole locations.
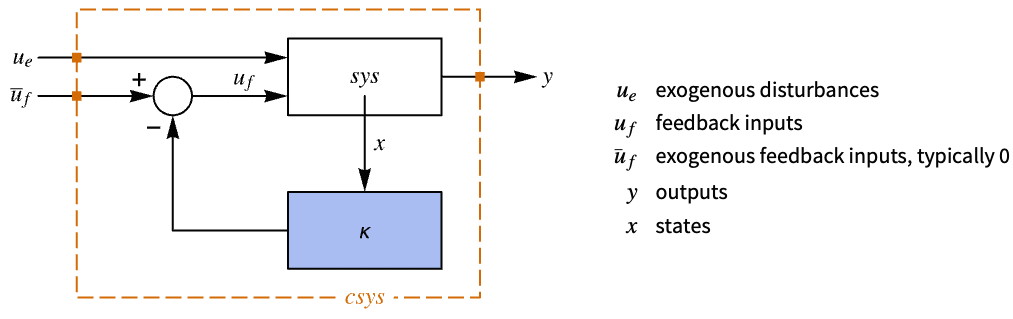
  • The system specification sspec is the system sys together with the uf, yt and yref specifications.
  • The system specification sspec can have the following forms:
  • StateSpaceModel[…]linear control input and linear state
    AffineStateSpaceModel[…]linear control input and nonlinear state
    NonlinearStateSpaceModel[…]nonlinear control input and nonlinear state
    SystemModel[…]general system model
    <|…|>detailed system specification given as an Association
  • The detailed system specification can have the following keys:
  • "InputModel"sysany one of the models
    "FeedbackInputs"Allthe feedback inputs uf
    "TrackedOutputs"Nonethe tracked outputs yt
    "TrackedSignal"Automaticthe dynamics of yref
  • The tracked signal dynamics is given as a function of the reference signal and time variable. By default, it is assumed to be constant.
  • Function[{r, t},r'[t]]continuous-time system
    Function[{r,k},r[k+1]-r[k]]discrete-time system
  • The feedback inputs and tracked outputs can have the following forms:
  • {num1,…,numn}numbered inputs numi used by StateSpaceModel, AffineStateSpaceModel and NonlinearStateSpaceModel
    {name1,…,namen}named inputs namei used by SystemModel
    Alluses all inputs
  • For nonlinear systems such as AffineStateSpaceModel, NonlinearStateSpaceModel and SystemModel, the system will be linearized around its stored operating point.
  • StateFeedbackGains[…,"Data"] returns a SystemsModelControllerData object cd that can be used to extract additional properties using the form cd["prop"].
  • StateFeedbackGains[…,"prop"] can be used to directly get the value of cd["prop"].
  • Possible values for properties "prop" include:
  • "ClosedLoopPoles"poles of the linearized "ClosedLoopSystem"
    "ClosedLoopSystem"system csys
    {"ClosedLoopSystem", cspec}detailed control over the form of the closed-loop system
    "ControllerModel"model cm
    "Design"type of controller design
    "DesignModel"model used for the design
    "FeedbackGains"gain matrix κ or its equivalent
    "FeedbackGainsModel"model gm or {gm1,gm2}
    "FeedbackInputs"inputs uf of sys used for feedback
    "InputModel"input model sys
    "InputCount"number of inputs u of sys
    "OpenLoopPoles"poles of "DesignModel"
    "OutputCount"number of outputs y of sys
    "SamplingPeriod"sampling period of sys
    "StateCount"number of states x of sys
    "TrackedOutputs"outputs yt of sys that are tracked
  • Possible keys for cspec include:
  • "InputModel"input model in csys
    "Merge"whether to merge csys
    "ModelName"name of csys
  • The diagram of the regulator layout.
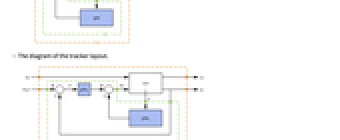
  • The diagram of the tracker layout.
  • StateFeedbackGains accepts a Method option with settings given by:
  • Automaticautomatic method selection
    "Ackermann"Ackermann method
    "KNVD"Kautsky–Nichols–Van Dooren method

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

The feedback gains for a system specification sspec with a feedback uf and exogenous input ue:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cg0873

A set of poles:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dkusag

The feedback gains:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-1yltm
Out[7]=7

The feedback gains for a nonlinear system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ba352z

The gains have an offset because of the nonzero operating points:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hrcg6r
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bjd2eu
Out[3]=3

The gains of the approximate linearized system do not have the offset:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-obnbd
Out[4]=4

Stabilize an unstable system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bdoz58
Out[1]=1

Compare the open-loop and closed-loop poles:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-kzoktx
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-endy04
Out[3]=3

Scope  (32)Survey of the scope of standard use cases

Basic Uses  (8)

Compute the state feedback gain that places the closed-loop pole at p:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-t5t5jm
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-n0fgnt
Out[2]=2

The closed-loop system has pole p:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2uwzt6
Out[3]=3

Compute the gain to stabilize an unstable system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bgp8e9
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-idq11v
Out[2]=2

The closed-loop system has pole :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-tgau8w
Out[3]=3

The unstable pole and the stabilized pole can be seen in the system's responses:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rln5wa

Compute the state feedback gains for a multiple-state system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ecq6tk
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-otxfdf
Out[2]=2

The dimensions of the result correspond to the number of inputs and the system's order:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bndtk0
Out[3]=3

Compute the gains for a system with 2 inputs and 3 states:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-woplly
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b00i4

Place the poles at conjugate pole locations:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-klha6i
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ysgyyj
Out[2]=2

If the poles are not complex conjugate, the gains will be complex:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-1p4aij
Out[3]=3

Place the poles at conjugate pole locations for a multiple-input system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-vdg14t
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ez99dq
Out[2]=2

If the poles are not complex conjugate, the control will be complex and use only one of the inputs:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bzger0
Out[3]=3

The first input is not used for feedback:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hql7tl
Out[4]=4

Choose the feedback inputs for multiple-input systems:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-0i4ngn

Choose the first input:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-01lb74
Out[2]=2

The second:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-knyktm
Out[3]=3

Both inputs:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-nptr8e
Out[4]=4

Compute the gains for a nonlinear system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gk820t

The controller is returned as a vector and takes operating points into consideration:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rh8rhe
Out[2]=2

The controller for the approximate linear system:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-d9v4y2
Out[3]=3

Plant Models  (6)

Continuous-time StateSpaceModel:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bl6t0x
Out[1]=1

Discrete-time StateSpaceModel:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-pg9u6j
Out[1]=1

Descriptor StateSpaceModel:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-svjmjx
Out[1]=1

AffineStateSpaceModel with no operating point is taken to be 0:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2sqhp9
Out[1]=1

NonlinearStateSpaceModel with no operating point is taken to be 0:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bbdtkg
Out[1]=1

SystemModel:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-priz8d
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lz5vvi
Out[2]=2

Properties  (10)

StateFeedbackGains returns the feedback gains by default:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b2vtn9
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-py3yi
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-n8g3ha
Out[4]=4

In general, the feedback is affine in the states:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-s4nzmh
Out[1]=1

It is of the form κ0+κ1.x, where κ0 and κ1 are constants:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-x99r1n
Out[2]=2

The systems model of the feedback gains:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6bgwzv
Out[1]=1

An affine feedback gains systems model:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-j5u9vm
Out[1]=1

The closed-loop system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-x5aaib
Out[1]=1

The poles of the linearized closed-loop system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2x7zcn
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8ow85o
Out[2]=2

They should be the specified poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-0v269u
Out[3]=3

The model used to compute the feedback gains:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-4p55s3
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ddqndd
Out[2]=2

The feedback gains of the input model and the design model, respectively:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cmf10r
Out[3]=3

The design method:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8rieu9
Out[1]=1

Properties related to the input model:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hhy36j
Out[1]=1

Get the controller data object:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-x4pozi
Out[1]=1

The list of available properties:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mlfinc
Out[2]=2

The value of a specific property:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-5hw1yx
Out[3]=3

Tracking  (5)

Design a tracking controller:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-5nafrb
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jno01f
Out[2]=2

The closed-loop system tracks the reference signal :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-labjao
Out[4]=4

Design a tracking controller for a discrete-time system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6ftl55
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-w9sp0
Out[2]=2

The closed-loop system tracks the reference signal :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b8ov75
In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dbimu6
Out[4]=4

Track multiple outputs:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-h9ptmy
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-njece0
Out[2]=2

The closed-loop system tracks two different reference signals:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8eqdsk
In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-s73ee9
Out[4]=4

Compute the controller effort:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-sf7r31
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-d4r25r
Out[2]=2

The controller model:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jn0yvo
Out[3]=3

The controller inputs:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2b6u51
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-74kmvc
Out[5]=5

The controller effort:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-qpbduu
Out[6]=6

Track a desired reference signal:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-t0y6q9
Out[1]=1

The reference signal is of order 2:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rgy3bg
Out[2]=2

And a sinusoid:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-h17nb8
Out[3]=3

Design a controller to track one output of a first-order system:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-uonosr
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gazp96
Out[5]=5

The number of pole specifications is k+m q:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-s3ojyk
Out[6]=6

Compute the controller:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-thj9va
Out[7]=7

The closed-loop system tracks the reference:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-7d0imb
Out[8]=8

Closed-Loop System  (3)

Assemble the closed-loop system for a nonlinear plant model:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-72bfia
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-loj504
Out[2]=2

The closed-loop system with a linearized model:

In[11]:=11
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6ic9u2
Out[11]=11

Compare the response of the two systems:

In[12]:=12
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-blj2li
Out[13]=13

Assemble the merged closed-loop of a plant with one disturbance and one feedback input:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-etddvq
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-qcwzrh
Out[2]=2

The unmerged closed-loop system:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lh5w9g
Out[3]=3

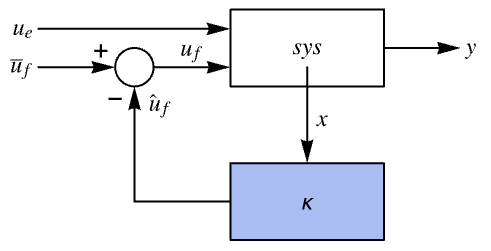
When merged, it gives the same result as before:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-smb8sz
Out[4]=4

Explicitly specify the merged closed-loop system:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gqdatj
Out[5]=5

Create a closed-loop system with a desired name:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-t8w608
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-yoybh6
Out[2]=2

The closed-loop system has the specified name:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-srctac
Out[3]=3

The name can be directly used to specify the closed-loop model in other functions:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-q4yvjv
Out[4]=4

The response simulation plot:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-g6dmea
Out[5]=5

Options  (6)Common values & functionality for each option

Method  (6)

The "Ackermann" method is used by default for systems with exact or symbolic values:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-db5rps
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hg16j
Out[3]=3

The "KNVD" method is used by default for inexact systems:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dokm4l
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-73r1z
Out[2]=2

LinearSolve is used for inexact systems with at least as many inputs as states:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-pmrsf
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cfnde0
Out[2]=2

The "KNVD" method is typically used for multi-input systems:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-t80goq
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-c2h3oz
Out[2]=2

The "Ackermann" method uses only one input for multi-input systems:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-oksp2p
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-9i7c9b
Out[2]=2

The second input is not used:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-vgsqvx
Out[3]=3

The input selected has the lowest controllability matrix condition number:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-oz6bmu
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-stioiv
Out[5]=5

The "KNVD" closed-loop poles are less sensitive to the feedback gain perturbations than "Ackermann":

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-16ik1f
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fnnvor
Out[2]=2

Add random perturbations to the gain matrices:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b061qo
Out[3]=3

The resulting closed-loop poles:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ep6hjj
Out[4]=4

The maximum error from the specified poles is smaller for the "KNVD" method:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-zg0sn3
Out[5]=5

Applications  (14)Sample problems that can be solved with this function

Mechanical Systems  (4)

Design a balancing controller for a Segway PT:

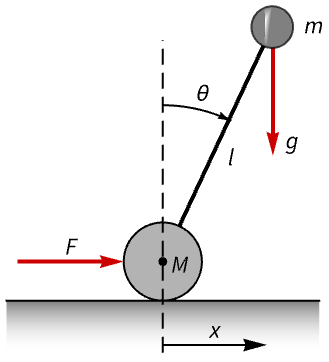
The nonlinear model of the Segway PT:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-evx3r8
Out[1]=1

Without a controller, the Segway's position and orientation are not balanced:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-eo9pn6
Out[3]=3

Design a controller to balance the Segway using pole placement:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jezmh9
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-k9y42t
Out[6]=6

Verify the closed-loop poles:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ba1b1m
Out[7]=7

The open-loop system was unstable:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-evzrh3
Out[8]=8

Obtain the closed-loop system:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bepvd9
Out[9]=9

It is balanced from a nonzero initial position:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cu9cxp
Out[11]=11

So is its response to a nudge:

In[12]:=12
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cd335h
Out[13]=13

Assess its control effort:

In[14]:=14
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dagr74
Out[15]=15

Design a regulator for a single-link robotic manipulator with a flexible joint:

A model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cc8ojn
Out[1]=1

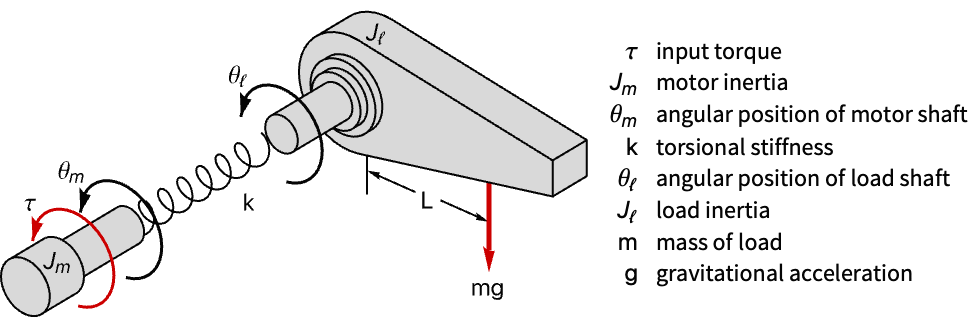
The arm's angular position is unregulated:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bm57ou
Out[2]=2

Design a state feedback controller:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gzlb32
Out[3]=3

Obtain the closed-loop system:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b0jz0q
Out[4]=4

The feedback controller regulates the arm's angular position:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6zw8c
Out[5]=5

Obtain the controller model:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bd06ik
Out[6]=6

The control effort:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fvigk6
Out[7]=7

Design a discrete-time stabilizing controller for a ball and beam system:

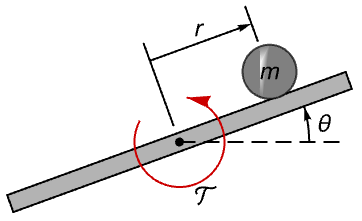
The linear continuous-time model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ibjbms
Out[1]=1

Discretize the model with a sampling period of :

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fmmh9f
Out[2]=2

The ball's position is unstable if the beam is perturbed:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-k7lq2h
Out[3]=3

Compute a stabilizing controller:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f1x4vs
Out[4]=4

Obtain the closed-loop system:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-pw5ta2
Out[5]=5

The ball's position is stabilized:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dcaaty
Out[6]=6

The control effort:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f2trub
Out[7]=7

Suppress the oscillations of a two-mass damper system:

The model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rm1lu
Out[1]=1

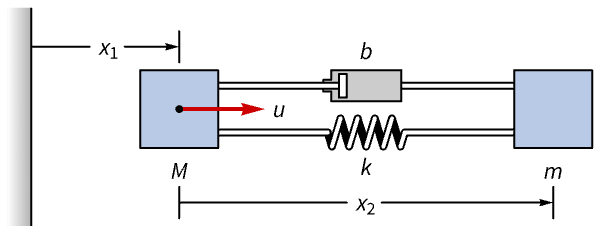
Discretize it with a sampling period of using the zero-order hold method:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hnt43o
Out[2]=2

The masses and oscillate when perturbed:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mrkbqm
Out[3]=3

Compute state feedback gains for a set of poles within the unit circle:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-q2bvy
Out[4]=4

Compute gains for a set of poles that are less damped:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fupg3z
Out[5]=5

Obtain the closed-loop systems for each set of poles:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-nrf0d0
Out[6]=6

Compare their responses to a perturbation:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jd2fye
In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-n4ddoy
Out[8]=8

Obtain the feedback gains:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-m7jg1a
Out[9]=9

Compare their control efforts:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fav1i
Out[10]=10

Electromechanical Systems  (1)

Dampen the oscillations on an angular gauge:

The model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-l3r6g8
Out[1]=1

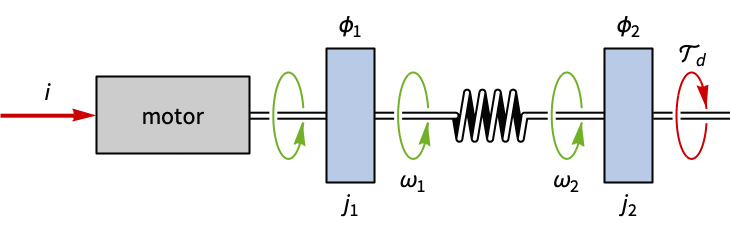
A disturbance of the gauge's position results in significant oscillations:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-4dceh
Out[3]=3

Set the current i as the feedback input:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fq2ux6

Design a state feedback controller to dampen the oscillations:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dxqp3e
Out[6]=6

Verify the closed-loop poles:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cbwx9m
Out[7]=7

Obtain the closed-loop system:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lcyobu
Out[8]=8

The oscillations are damped:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jxkm0
Out[10]=10

A sinusoidal torque disturbance is also blocked by the controller:

In[23]:=23
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mv4kkw
Out[24]=24

Obtain the controller model:

In[13]:=13
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f4l1l6
Out[13]=13

Its control effort:

In[14]:=14
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-eun3rc
Out[15]=15

Aerospace Systems  (2)

Improve the handling of an aircraft's response about the longitudinal axis:

The model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-7yfju
Out[1]=1

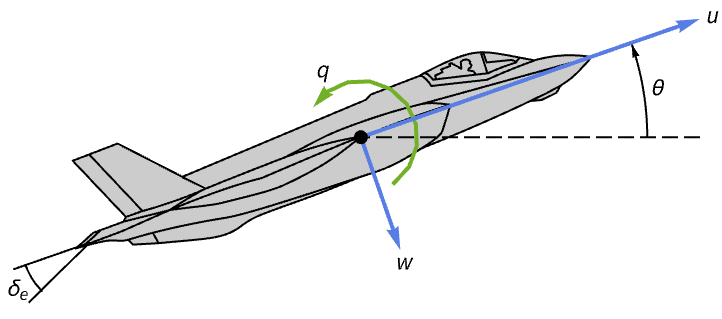
Its pitch angle takes about 1500 seconds to stabilize after an initial perturbation:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dxbxpf
Out[3]=3

Design a controller to improve the response:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-de8tdw
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-m75qx
Out[6]=6

Obtain the closed-loop system:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cln9r6
Out[7]=7

The response of the closed-loop system now stabilizes in about 10 seconds:

In[14]:=14
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-d4ej5h
Out[15]=15

Obtain the controller model:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cfjem1
Out[10]=10

The controller effort:

In[11]:=11
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-judzj
In[12]:=12
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gs5yth
Out[12]=12

Design an output feedback controller to regulate an orbiting satellite's trajectory:

A model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ec3r9z
Out[1]=1

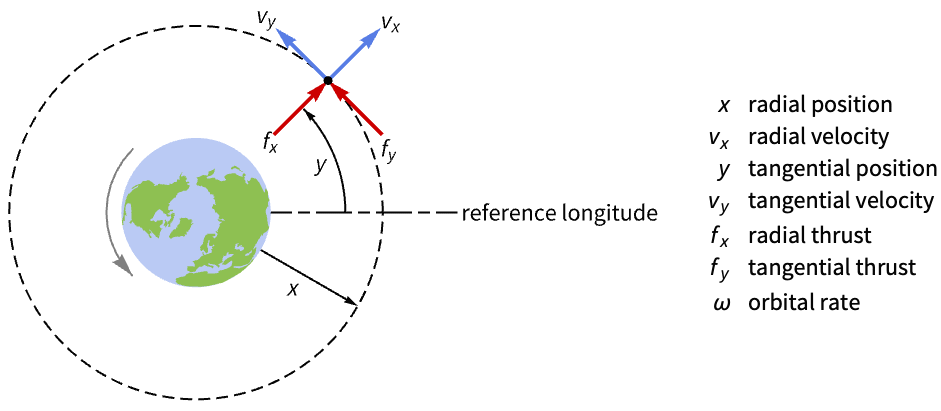
The orbit is unstable if perturbed:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ey529o
Out[2]=2

Compute a set of feedback gains:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lca66p

Compute a set of estimator gains:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-c1yb3d

Assemble the estimator regulator:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cofutv
Out[5]=5

Obtain the closed-loop system:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b6qbep
Out[6]=6

Compute the response of the closed-loop system:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f2gy21
Out[7]=7

Obtain the controller model:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-l2x7sr
Out[8]=8

Plot the control effort:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8hkln
Out[9]=9

Electrical Systems  (3)

Tune the frequency response of a circuit:

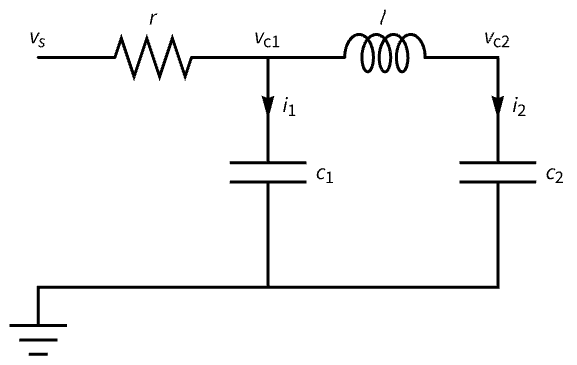
A descriptor model of the circuit:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b62mwf
Out[1]=1

Its step response is highly oscillatory:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b6dlje
Out[3]=3

The oscillatory response is due to its underdamped poles:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ei19m1
Out[4]=4

Design a state feedback controller with poles that are not underdamped:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-csga9k
Out[6]=6

Obtain the closed-loop system:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bgn6ej
Out[7]=7

The oscillations are damped:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fzt6sh
Out[9]=9

Compare the frequency responses of the open- and closed-loop systems:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-osgx50
Out[10]=10

The control effort:

In[11]:=11
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hefe1x
Out[11]=11

Tune an active bandpass filter:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-d69rlr
Out[1]=1

A state-space realization of the filter:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gc4x9w
Out[2]=2

Its poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-nsl70
Out[3]=3

Design a set of controllers to improve the filter's characteristics:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-c4p7dz
Out[4]=4

The more damped the poles are, the smaller the oscillations:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gofoqi
Out[5]=5

Design a speed controller for a DC motor:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-kcjcr9
Out[1]=1

Set the motor speed as a tracked output:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f49y88
Out[2]=2

Compute a pole placement controller:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hz410p
Out[3]=3

Compute an estimator:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-e62p88
Out[4]=4

Assemble an estimator regulator that tracks the motor velocity:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ey6y2
Out[5]=5

The closed-loop system:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bstgvm
Out[6]=6

The response to a reference speed of rpm:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hu3429
In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mj56l
Out[8]=8

The controller effort:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cycyqn
Out[9]=9

It is volts:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6w090
Out[10]=10

Chemical Systems  (2)

Improve the response of the flow rate in a mixing tank:

A model of the system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bdpdzc
Out[1]=1

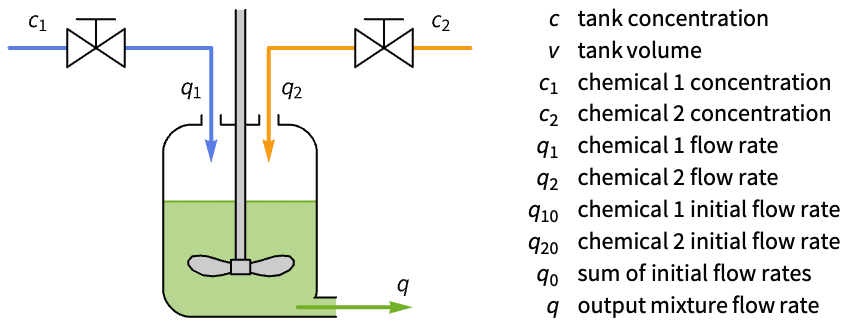
The response to a disturbance in the flow rate q2 is sluggish:

In[20]:=20
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-btgxuz
Out[21]=21

Design a state feedback controller to accelerate the response:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ggyzg9
Out[4]=4

The closed-loop system:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-g0d3nw
Out[5]=5

The response of the closed-loop system is faster:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gxfq10
Out[7]=7

Obtain the feedback gains:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cg9y3m
Out[8]=8

The control effort:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fbfat3
Out[9]=9

Improve the response of a two-stage chemical reactor with delayed recycle:

A model of the reactor:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hhbkwe
Out[1]=1

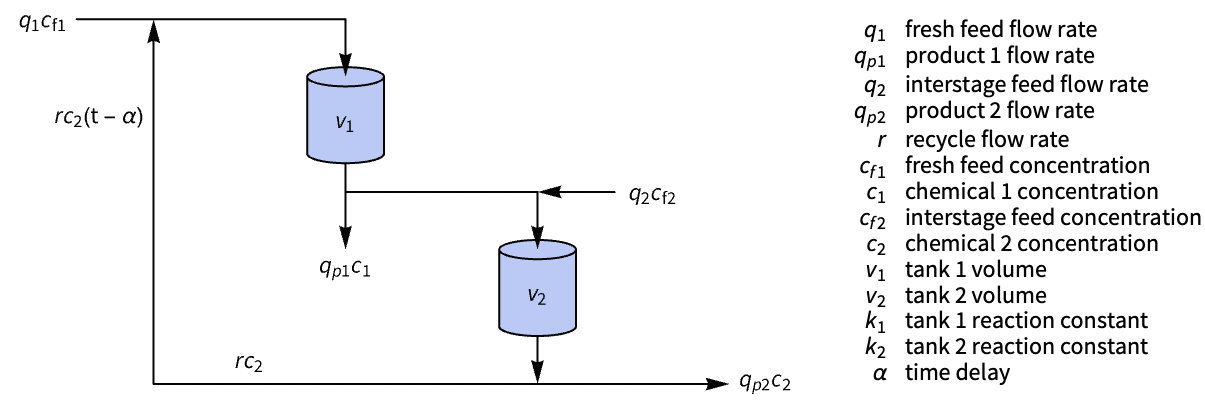
The reactor's response to a perturbation is delayed:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-h23p4d
Out[2]=2

Remove the delay and obtain a minimal realization of the model:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ehuzay
Out[3]=3

Compute a set of regulator gains:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b79xv
Out[4]=4

And a set of estimator gains:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-fb4grr
Out[5]=5

Assemble the estimator regulator using the computed gains:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-0lr3z
Out[6]=6

Assemble a Smith compensator for the original system:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-eb49g
Out[7]=7

Obtain the closed-loop system of the model with the Smith compensator in the feedback path:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cg0btd
Out[8]=8

The closed-loop response to an initial perturbation has been improved:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ifx00h
Out[9]=9

Deadbeat Control  (1)

Solve the deadbeat control problem for a discrete-time system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-s7uan

The closed-loop system with all poles at the origin:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-flda2u
Out[2]=2

The order of the open-loop system is :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-7bra46
Out[3]=3

Thus the closed-loop system's outputs are zero within three steps:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cnpfhi
Out[4]=4

Its plot:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-xdqspb
Out[5]=5

Nautical Systems  (1)

Design a controller for a boat to track a desired heading angle:

A model of the boat:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-blfkrl
Out[1]=1

Design a tracking controller with poles at the desired locations:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jpfvki
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-iqkese
Out[3]=3

The closed-loop system:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dmzb2s
Out[4]=4

The response for various heading angle references:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-g5spyp
Out[6]=6

Obtain the controller model:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mrkp4x
Out[7]=7

The controller inputs:

In[9]:=9
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cky7qo

The control effort increases as the reference value increases:

In[10]:=10
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-i8gjym
Out[11]=11

Properties & Relations  (17)Properties of the function, and connections to other functions

The state feedback gains are computed for negative feedback:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8uio9z
In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-khh89p
Out[4]=4

The closed-loop poles with negative feedback -κ.x:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mhugiz
Out[5]=5

They are the same as the specified poles:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gwwfo3
Out[6]=6

The closed-loop system is obtained using state feedback:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-kab4jo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f96jnd
Out[2]=2

Obtain it directly as a property:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ltpav
Out[3]=3

The control effort increases as the closed-loop poles are moved further away from the open-loop poles:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-uozxo5
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-qmsej9
Out[2]=2

For a nonlinear system the gains are affine and of the form :

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-c81l8

The affine gains:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-iur93b
Out[2]=2

The gains of the linearized system are linear of the form :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-m0cejt
Out[3]=3

The affine gains are obtained by solving :

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-vjl299
Out[4]=4

All the poles of a controllable standard StateSpaceModel can be controlled using state feedback:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-y79pg9
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2ay05f
Out[2]=2

A set of new stable poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-yxa3ew
Out[3]=3

The gains of the controller:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rs40qs
Out[4]=4

The closed-loop poles are the specified poles:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hyivd3
Out[5]=5

All the poles of a controllable nonsingular descriptor StateSpaceModel can also be controlled:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ddh2mc
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8rzopx
Out[2]=2

A set of new stable poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-d9ce9j
Out[3]=3

The gains of the controller:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-1mbs8g
Out[4]=4

The closed-loop poles are the specified poles:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-58sc7d
Out[5]=5

Only a subsystem of an an uncontrollable standard StateSpaceModel can be controlled:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-3hvjdc

The eigenvalue is controllable and is not:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ig0gj0
Out[2]=2

Move only the controllable eigenvalue to :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-52vuc9
Out[3]=3

It is not possible to move the uncontrollable eigenvalue:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-9rmv4s
Out[4]=4

Only the poles of the controllable slow subsystem of a nonsingular descriptor can be controlled:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-qry0id
Out[1]=1

The dimension of the slow subsystem:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-i61hl0
Out[2]=2

A new stable pole:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lz9amy
Out[3]=3

The gain corresponding to the fast subsystem is :

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8tu84k
Out[4]=4

The pole of the slow subsystem is moved to the desired location and the pole at corresponding to the fast subsystem is unchanged:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-w46xk7
Out[5]=5

The complete system is uncontrollable and is of order less than the number of states:

In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-p61v8u
Out[6]=6

None of the poles of the controllable slow subsystem of a nonsingular descriptor can be controlled:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-1lwfx
Out[1]=1

The dimension of the slow subsystem:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-i1m1ca
Out[2]=2

A new stable pole:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-kpxim9
Out[3]=3

None of the poles are changed:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-2uejqg
Out[4]=4

LQRegulatorGains and StateFeedbackGains yield the same results for a single-input system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hbvbed

StateFeedbackGains with the closed-loop poles of the LQRegulatorGains design:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f8hxrg
Out[2]=2

LQRegulatorGains gives the same gains:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bo4qou
Out[3]=3

The closed-loop poles that minimize ρ c.c x(t)2+u(t)2t can be obtained using the symmetric root locus plot:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bz21jf

The symmetric root locus plot:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-yb5f8j
Out[2]=2

The closed-loop poles for the parameter value :

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bqumeo
Out[3]=3

The feedback gains to place the poles at the specified locations:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ke2dum
Out[4]=4

The same gains are obtained using LQRegulatorGains:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-4ntuj4
Out[5]=5

For a StateSpaceModel, StateFeedbackGains and FullInformationOutputRegulator give the same results:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-n27jbz
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-hn5x1d
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cjoiaa
Out[3]=3

An estimator regulator is assembled using state feedback and estimator gain matrices:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-n9iqfg
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f9hp57
Out[2]=2

The estimator regulator with the computed gains:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-772k05
Out[3]=3

State feedback gains correspond to the gain in the closed-loop system for single-input systems:

The closed-loop poles for a gain value κ:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dconhg
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jpzhut
Out[2]=2

The controllable canonical state-space realization of the system:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-xnq1k
Out[3]=3

For this realization, the state feedback gains are of the form {{κ,0,…,0}}:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-f5ezr7
Out[4]=4

The closed-loop poles for a gain value κ:

In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-pt9jdg
In[6]:=6
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b0alig
Out[6]=6

The controllable canonical state-space realization of the system:

In[7]:=7
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-w69u5z
Out[7]=7

For this realization, the state feedback gains are of the form {{κ,0,…,0}}:

In[8]:=8
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-i9f7qy
Out[8]=8

The state feedback and estimator gains are duals of each other:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-8aiupx
Out[1]=1

The state feedback gains of the system for a set of poles:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-b45r4z
Out[2]=2

The estimator gains of the dual system for the conjugate set of poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-rgs5n6
Out[3]=3

The state feedback gain matrix is the conjugate transpose of the estimator gain matrix and conversely:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6bl8o7
Out[4]=4

State feedback does not alter the input-blocking properties of a system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jvd2dy

The zeros of the system:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-c40di0
Out[2]=2

The closed-loop system for a specific set of poles:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-lq1gkq
Out[3]=3

Both the open- and closed-loop systems block the input Sin[2t]:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-pj40u
Out[4]=4

The closed-loop system becomes unobservable if the state feedback makes a pole and a zero coincident:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-6hoesd
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bcams2
Out[2]=2

The closed-loop system with the pole coinciding with the zero:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-mqcdgs
Out[3]=3

The coincident pole-zero pair makes the closed-loop system unobservable:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-7b3hcm
Out[4]=4

Possible Issues  (5)Common pitfalls and unexpected behavior

The gains cannot be calculated for an uncontrollable system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-4ip8gh
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-u0owbx
Out[3]=3

An uncontrollable descriptor system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-ds4zzl
Out[1]=1

The dimension of the slow subsystem:

In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-0l5ag
Out[2]=2

None of the poles are changed:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-0r7ck0
Out[3]=3

The gains cannot be calculated for an unstabilizable system:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-56s2os
Out[1]=1

The KNVD method does not handle exact systems with fewer inputs than states:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-knil2v
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-jcq991
Out[2]=2

Evaluate numerically:

In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-bse53e
Out[3]=3

Or use the Ackermann method:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-08qnnv
Out[4]=4

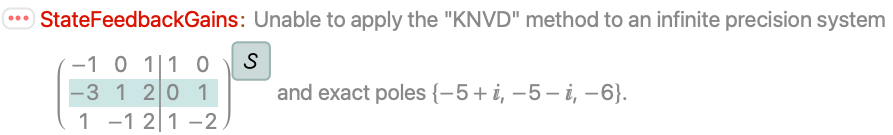
The KNVD method can give different sets of gains on different computer systems:

In[1]:=1
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-cl3qxh
In[2]:=2
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-dendz1
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-gfo0d0
Out[3]=3

The closed-loop eigenvalues are the same:

In[4]:=4
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-7yb93
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0coknw44935agctvuxlg-kfm5j1
Out[5]=5
Wolfram Research (2010), StateFeedbackGains, Wolfram Language function, https://reference.wolfram.com/language/ref/StateFeedbackGains.html (updated 2021).
✖
Wolfram Research (2010), StateFeedbackGains, Wolfram Language function, https://reference.wolfram.com/language/ref/StateFeedbackGains.html (updated 2021).

Text

Wolfram Research (2010), StateFeedbackGains, Wolfram Language function, https://reference.wolfram.com/language/ref/StateFeedbackGains.html (updated 2021).

✖
Wolfram Research (2010), StateFeedbackGains, Wolfram Language function, https://reference.wolfram.com/language/ref/StateFeedbackGains.html (updated 2021).

CMS

Wolfram Language. 2010. "StateFeedbackGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/StateFeedbackGains.html.

✖
Wolfram Language. 2010. "StateFeedbackGains." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/StateFeedbackGains.html.

APA

Wolfram Language. (2010). StateFeedbackGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateFeedbackGains.html

✖
Wolfram Language. (2010). StateFeedbackGains. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateFeedbackGains.html

BibTeX

@misc{reference.wolfram_2025_statefeedbackgains, author="Wolfram Research", title="{StateFeedbackGains}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/StateFeedbackGains.html}", note=[Accessed: 07-June-2025 ]}

✖
@misc{reference.wolfram_2025_statefeedbackgains, author="Wolfram Research", title="{StateFeedbackGains}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/StateFeedbackGains.html}", note=[Accessed: 07-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_statefeedbackgains, organization={Wolfram Research}, title={StateFeedbackGains}, year={2021}, url={https://reference.wolfram.com/language/ref/StateFeedbackGains.html}, note=[Accessed: 07-June-2025 ]}

✖
@online{reference.wolfram_2025_statefeedbackgains, organization={Wolfram Research}, title={StateFeedbackGains}, year={2021}, url={https://reference.wolfram.com/language/ref/StateFeedbackGains.html}, note=[Accessed: 07-June-2025 ]}