EstimatorGains

EstimatorGains[ssm,{p1,p2,…,pn}]

给出 StateSpaceModel ssm 的估值器增益矩阵，以使得估值器的极点是 pi.

EstimatorGains[{ssm,{out1,…}},…]

指定使用的测量输出 outi.

更多信息和选项

  • EstimatorGains 也称为观测器增益或者观测器极点位置.
  • 状态空间模型 ssm 可以以 StateSpaceModel[{a,b,c,d}] 的形式给出，其中 a、b、c 和 d 分别表示在连续时间系统或者离散时间系统中的状态、输入、输出和传递矩阵：
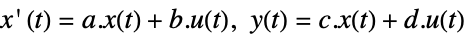
  • 连续时间系统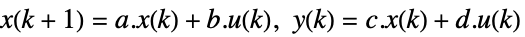
    离散时间系统
  • 如果 ssm 是能观测的，那么 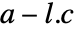的特征值为 {p1,p2,…,pn}，其中 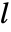是计算所得的估值器增益矩阵.
  • 对于描述器系统 StateSpaceModel[{a,b,c,d,e}]，可以指定的极点数目由 e 的阶数和系统的可观测性决定. »
  • EstimatorGains 也接受由 AffineStateSpaceModel 和 NonlinearStateSpaceModel 指定的非线性系统.
  • 对于非线性系统，考虑状态和输入变量的操作值，并且给予近似泰勒线性化计算增益.
  • EstimatorGains[{ssm,{out1,…}},…] 等价于 EstimatorGains[ssm1,…]，其中ssm1SystemsModelExtract[ssm,All,{out1,…}].
  • 观测器动态特性由下面的方程给出：
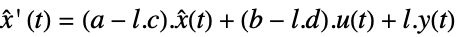
  • 连续时间系统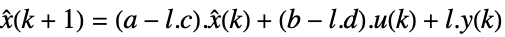
    离散时间系统
  • 若 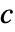是一个非奇异方矩阵，状态向量可以通过如下方式计算：x=TemplateBox[{c}, Inverse].(y-d.u).
  • EstimatorGains 接受 Method 选项，其中设置由下面给出：
  • Automatic自动方法选择
    "Ackermann"Ackermann 方法
    "KNVD"Kautsky–Nichols–Van Dooren 方法
  • 估值器增益根据对偶系统的状态反馈增益计算.

范例

打开所有单元关闭所有单元

基本范例  (3)

计算一个连续时间系统的估值器增益：

一个离散时间系统：

只有第二个输出已测量的双输出系统的估值器增益：

范围  (6)

一个 SISO 系统的增益集合：

对解进行验证：

一个双输出系统的观测器增益矩阵：

具有指定测量值的三输出系统的估值器增益矩阵：

计算估值器增益，其中把极点指定为一个多项式的根：

以符号形式确定估值器增益：

计算 AffineStateSpaceModel 的增益：

合成估值器：

估值器极点位于期望的位置上：

选项  (6)

Method  (6)

对于输出比状态更多的系统，Automatic 使用 LinearSolve 求增益：

对于具有精确值的系统，默认情况下采用 Ackermann 方法：

Ackermann 方法也用于符号式数值：

对于数值系统，Automatic 使用 "KNVD" 方法：

一个不精确，多输出状态空间模型和期望估值器极点位置：

对第一个输入，求可观测矩阵的条件数目：

对第二个输入，求可观测矩阵的条件数目：

默认情况下，选择具有最低条件数目的输出：

通过第一个输出，求估计增益：

KNVD 方法使用所有可得到的输出来估计状态：

应用  (2)

构建一个连续时间系统的观测器：

从一个随机初始条件开始，模拟输入为 Sin[t] 的系统：

比较每个状态和它的估计值：

对一个零输入采样数据系统，构建一个观测器：

对于初始状态 {1,–0.75,0.5} 和初始观测器状态 {0,0,0}，计算实际和估计状态：

检查由观测器获得的状态跟踪：

属性和关系  (7)

误差动态：

StateOutputEstimator 组建了一个可以同时估计状态和输出的观测器：

离散时间系统的预测估值器动态：

估值器增益是对偶系统的状态反馈增益的共轭转置：

反之亦然：

F对于可观测非奇异描述器系统，可以放置所有估值器极点：

对于可观测奇异系统，只可以放置 MatrixRank[e] 极点：

脉冲系统，只有缓慢子系统可观测：

只可以放置慢速系统的估值器极点：

可能存在的问题  (4)

KNVD 方法无法处理输出比状态少的精确系统：

数值形式的计算：

KNVD 方法不支持极点重数大于输出数目：

使用 Ackermann 方法：

KNVD 方法可以给出不同计算机系统上的不同增益集合：

观测器的特征值是相同的：

该系统必须是能观测的：

经检查，该系统是不能观测的：

Wolfram Research (2010)，EstimatorGains，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EstimatorGains.html （更新于 2014 年）.

文本

Wolfram Research (2010)，EstimatorGains，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EstimatorGains.html （更新于 2014 年）.

CMS

Wolfram 语言. 2010. "EstimatorGains." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2014. https://reference.wolfram.com/language/ref/EstimatorGains.html.

APA

Wolfram 语言. (2010). EstimatorGains. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EstimatorGains.html 年

BibTeX

@misc{reference.wolfram_2024_estimatorgains, author="Wolfram Research", title="{EstimatorGains}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/EstimatorGains.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_estimatorgains, organization={Wolfram Research}, title={EstimatorGains}, year={2014}, url={https://reference.wolfram.com/language/ref/EstimatorGains.html}, note=[Accessed: 17-November-2024 ]}