EulerCharacteristic

EulerCharacteristic[poly]

gives the Euler characteristic of a poly.

Details

  • EulerCharacteristic is also known as Euler number or Euler–Poincaré characteristic.
  • EulerCharacteristic is a topological invariant that describes the shape of the polyhedron, regardless of the way it is bent.
  • The Euler characteristic 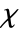for a polyhedron is given by 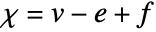, where 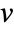is the number of vertices, 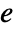the number of edges and 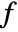the number of faces.
  • A polyhedron with 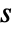voids and 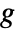tunnels satisfies .
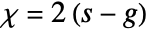  • The Euler characteristic for a mesh region is given by χ=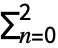(-1)nMeshCellCount[poly,n].

Examples

open allclose all

Basic Examples  (1)

Euler characteristic of a polyhedron:

Scope  (4)

EulerCharacteristic works on polyhedrons:

Tetrahedron:

Hexahedron:

Polyhedron with holes:

Polyhedrons with disconnected components:

EulerCharacteristic works on mesh regions:

Properties & Relations  (3)

Use EulerCharacteristic to compute PolyhedronGenus for a simple polyhedron:

Euler characteristic of a convex polyhedron equals 2:

Euler characteristic of UniformPolyhedron is 2:

Wolfram Research (2019), EulerCharacteristic, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

Text

Wolfram Research (2019), EulerCharacteristic, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

CMS

Wolfram Language. 2019. "EulerCharacteristic." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

APA

Wolfram Language. (2019). EulerCharacteristic. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerCharacteristic.html

BibTeX

@misc{reference.wolfram_2023_eulercharacteristic, author="Wolfram Research", title="{EulerCharacteristic}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/EulerCharacteristic.html}", note=[Accessed: 22-September-2023 ]}

BibLaTeX

@online{reference.wolfram_2023_eulercharacteristic, organization={Wolfram Research}, title={EulerCharacteristic}, year={2019}, url={https://reference.wolfram.com/language/ref/EulerCharacteristic.html}, note=[Accessed: 22-September-2023 ]}