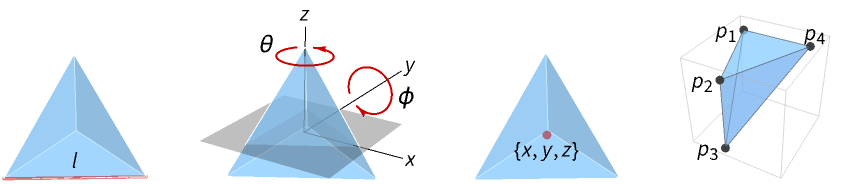
represents a regular tetrahedron centered at the origin with unit edge length.
Tetrahedron[l]
represents a tetrahedron with edge length l.
Tetrahedron[{θ,ϕ},…]
represents a tetrahedron rotated by an angle θ with respect to the z axis and angle ϕ with respect to the y axis.
Tetrahedron[{x,y,z},…]
represents a tetrahedron centered at {x,y,z}.
Tetrahedron[{p1,p2,p3,p4}]
represents a general filled tetrahedron with corners p1, p2, p3 and p4.
Tetrahedron[{{p1,1,p1,2,p1,3,p1,4},{p2,1,…},…}]
represents a collection of tetrahedra.


Tetrahedron
represents a regular tetrahedron centered at the origin with unit edge length.
Tetrahedron[l]
represents a tetrahedron with edge length l.
Tetrahedron[{θ,ϕ},…]
represents a tetrahedron rotated by an angle θ with respect to the z axis and angle ϕ with respect to the y axis.
Tetrahedron[{x,y,z},…]
represents a tetrahedron centered at {x,y,z}.
Tetrahedron[{p1,p2,p3,p4}]
represents a general filled tetrahedron with corners p1, p2, p3 and p4.
Tetrahedron[{{p1,1,p1,2,p1,3,p1,4},{p2,1,…},…}]
represents a collection of tetrahedra.
Details and Options

- Tetrahedron is also known as regular tetrahedron or triangular pyramid.
- Tetrahedron can be used as a geometric region and as a graphics primitive.
- Tetrahedron[] is equivalent to Tetrahedron[{0,0,0},1].
- Tetrahedron[l] is equivalent to Tetrahedron[{0,0,0},l].
- Tetrahedron[{p1,p2,p3,p4}] represents the region consisting of all the convex combinations of corner points pi,
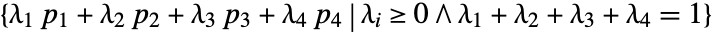 .
. - CanonicalizePolyhedron can be used to convert a tetrahedron to an explicit Polyhedron object.
- Tetrahedron can be used in Graphics3D.
- In graphics, the points and edge lengths can be Scaled and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, Texture, and color.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures
Examples
open all close allScope (19)
Graphics (9)
Styling (3)
FaceForm and EdgeForm can be used to specify the styles of the faces and edges:
Apply a Texture to the faces:
Assign VertexColors to vertices:
Coordinates (3)
Specify coordinates by fractions of the plot range:
Specify scaled offsets from the ordinary coordinates:
Points can be Dynamic:
Regions (10)
Embedding dimension is the dimension of the space in which the tetrahedron lives:
Geometric dimension is the dimension of the shape itself:
Get conditions for membership:
The equidistance contours for a tetrahedron:
Nearest points to an enclosing sphere:
Integrate over a tetrahedron region:
Applications (5)
The standard tetrahedron is given by points ![]() :
:
A Kuhn tetrahedron is given by points ![]() :
:
Define a regular tetrahedron by a radius from its center to a corner:
Create a compound of two regular tetrahedra:
If the four faces of a tetrahedron have the same area, then it is an isosceles tetrahedron:
Compare the area of each face:
Properties & Relations (8)
TriangulateMesh can be used to decompose a volume mesh into tetrahedra:
Use options such as MaxCellMeasure to control the number of tetrahedra:
A hexahedron can be represented as the union of five tetrahedra:
Point index list of tetrahedra vertices:
A hexahedron can also be represented as the union of six tetrahedra:
Any tetrahedron is an affine transformation of the standard tetrahedron:
The transformation is given by ![]() , where
, where ![]() :
:
Compare original and transformed unit tetrahedron:
Tetrahedron is a special case of Simplex:
ImplicitRegion can represent any Tetrahedron region:
Tetrahedron is the set of convex combinations of its vertices:
Vertices of a Tetrahedron can be used to form an enclosing Circumsphere:
Related Guides
Text
Wolfram Research (2014), Tetrahedron, Wolfram Language function, https://reference.wolfram.com/language/ref/Tetrahedron.html (updated 2019).
CMS
Wolfram Language. 2014. "Tetrahedron." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Tetrahedron.html.
APA
Wolfram Language. (2014). Tetrahedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Tetrahedron.html
BibTeX
@misc{reference.wolfram_2025_tetrahedron, author="Wolfram Research", title="{Tetrahedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Tetrahedron.html}", note=[Accessed: 19-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_tetrahedron, organization={Wolfram Research}, title={Tetrahedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Tetrahedron.html}, note=[Accessed: 19-January-2026]}