EulerCharacteristic

EulerCharacteristic[poly]

给出 poly 的欧拉示性数.

更多信息

  • EulerCharacteristic 亦成为欧拉数或 Euler–Poincaré 示性数.
  • EulerCharacteristic 是一个描述多面体形状的拓扑不变量，不考虑它弯曲的方式.
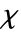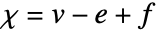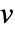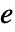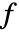  • 多面体的欧拉示性数 由 给出，其中 是顶点数， 为边数， 为面数.
  • 有 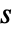个洞和 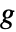个巷道的多面体满足 .
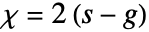  • 网格区域的欧拉示性数由 χ=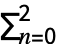(-1)nMeshCellCount[poly,n] 给出.

范例

打开所有单元关闭所有单元

基本范例  (1)

多面体的欧拉示性数：

范围  (4)

EulerCharacteristic 适用于多面体：

Tetrahedron：

Hexahedron：

有洞的多面体：

有断开组件的多面体：

EulerCharacteristic 适用于网格区域：

属性和关系  (3)

用 EulerCharacteristic 计算简单多面体的 PolyhedronGenus：

凸多面体的欧拉示性数等于 2：

UniformPolyhedron 的欧拉示性数为 2：

Wolfram Research (2019)，EulerCharacteristic，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

文本

Wolfram Research (2019)，EulerCharacteristic，Wolfram 语言函数，https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

CMS

Wolfram 语言. 2019. "EulerCharacteristic." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/EulerCharacteristic.html.

APA

Wolfram 语言. (2019). EulerCharacteristic. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/EulerCharacteristic.html 年

BibTeX

@misc{reference.wolfram_2024_eulercharacteristic, author="Wolfram Research", title="{EulerCharacteristic}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/EulerCharacteristic.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_eulercharacteristic, organization={Wolfram Research}, title={EulerCharacteristic}, year={2019}, url={https://reference.wolfram.com/language/ref/EulerCharacteristic.html}, note=[Accessed: 22-November-2024 ]}