ExponentialFamily

ExponentialFamily

GeneralizedLinearModelFitのオプションで，モデルの指数分布族を与える．

詳細

  • ExponentialFamilyは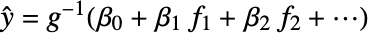，でモデル化される独立した観測値 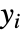の予測される分布を明記する．
  • 指数分布族の密度関数は，関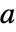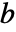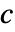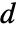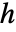数 ，，，， 確率変数 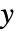，正準パラメータ 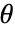，分散パラメータ 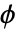について 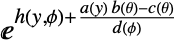の形式で書くことができる．
  • パラメータ分布の可能な値には"Binomial"，"Poisson"，"Gamma"，"Gaussian"，"InverseGaussian"がある．
  • 観察された応答 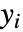は次のようなパラメータ分布の領域に限定される．
  • "Binomial"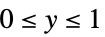
    "Gamma"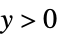
    "Gaussian"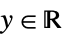
    "InverseGaussian"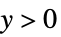
    "Poisson"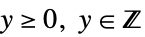
  • ExponentialFamily->"QuasiLikelihood"の設定で最尤度フィットを使用する擬似尤度関数を定義する．
  • 応答 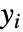と予測 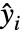についての対数擬似尤度関数は 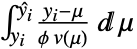で与えられる．ただし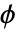， は分散パラメータ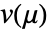，は分散関数である．分散パラメータは入力データから推定され，オプションDispersionEstimatorFunctionで制御することができる．
  • ExponentialFamily->{"QuasiLikelihood",opts}の設定で，次のような擬似尤度サブオプションが指定できる．
  • "ResponseDomain"Function[y,y>0]応答 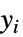の領域
    "VarianceFunction"Function[μ,1]平均の関数としての分散
  • パラメータ分布は次の"VarianceFunction"と"ResponseDomain" のサブオプションを使った擬似尤度構造としてエミュレートすることができる．
  • "Binomial"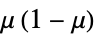0<=y<=1
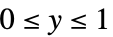
    "Gamma"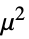
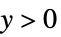
    "Gaussian"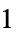
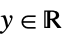
    "InverseGaussian"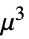
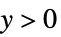
    "Poisson"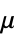
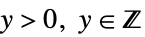
  • "Binomial"と"Poisson"族の"QuasiLikelihood"異形は，理論的な分散(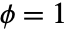)とは異なる過分散(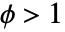)および分散不足 (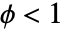)のデータモデルに使うことができる．
  • よく使われる分散関数，応答領域，用途は次の通りである．
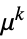
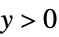
  • 電力モデル，保険数理，気象学等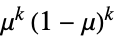
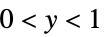
    確率モデル，二項関連等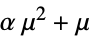
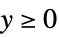
    モデルの数え上げ，ポアソン関連等

例題

すべて開くすべて閉じる

例  (1)

データを簡単な線形回帰モデルにフィットする：

正準ガンマ回帰モデルにフィットする：

正準逆ガウス回帰モデルにフィットする：

スコープ  (2)

"Binomial"族を確率のロジットモデルに使う：

"Poisson"をデータの数え上げの対数線形モデルに使う：

特性と関係  (3)

デフォルトのExponentialFamilyとLinkFunctionはLinearModelFitにマッチする：

デフォルトの"Binomial"モデルはLogitModelFitにマッチする：

"Gamma"モデルと"QuasiLikelihood"の類推をフィットする：

モデルは名前付きの類推から"LogLikelihood"中の定数分だけ異なる：

フィットしたパラメータは一致する：

対数尤度の差に基づいた結果は一致する：

Wolfram Research (2008), ExponentialFamily, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExponentialFamily.html.

テキスト

Wolfram Research (2008), ExponentialFamily, Wolfram言語関数， https://reference.wolfram.com/language/ref/ExponentialFamily.html.

CMS

Wolfram Language. 2008. "ExponentialFamily." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialFamily.html.

APA

Wolfram Language. (2008). ExponentialFamily. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialFamily.html

BibTeX

@misc{reference.wolfram_2024_exponentialfamily, author="Wolfram Research", title="{ExponentialFamily}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExponentialFamily.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_exponentialfamily, organization={Wolfram Research}, title={ExponentialFamily}, year={2008}, url={https://reference.wolfram.com/language/ref/ExponentialFamily.html}, note=[Accessed: 22-November-2024 ]}