ExponentialFamily

ExponentialFamily

GeneralizedLinearModelFit 的选项，它指定模型的指数族.

更多信息

  • ExponentialFamily 指定由 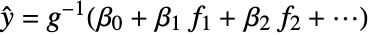指定独立 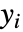观察模型的假定分布.
  • 一个指数族的密度函数以形式 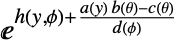写入，其中 a、b、c、d 和 h 为函数，y 是随机变量， θ 是标准参数， ϕ 是扩散参数.
  • 可能的参数分布包含："Binomial"、"Poisson"、"Gamma"、"Gaussian"、"InverseGaussian".
  • 观察响应 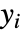限制在下列参数分布的域内：
  • "Binomial"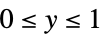
    "Gamma"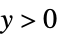
    "Gaussian"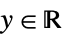
    "InverseGaussian"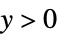
    "Poisson"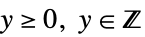
  • 设置 ExponentialFamily->"QuasiLikelihood"，定义半概率函数，用于一个最大概似法.
  • 响应 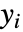、 预测 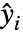的对数逆似然函数由 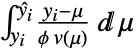给出，其中 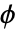是散布参数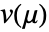， 是方差函数. 散步参数可以从输入估计得出，并通过选项 DispersionEstimatorFunction 来控制.
  • 设置 ExponentialFamily->{"QuasiLikelihood",opts} 允许指定下列拟似然子选项：
  • "ResponseDomain"Function[y,y>0]响应 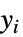的域
    "VarianceFunction"Function[μ,1]方差
  • 通过 "VarianceFunction" 和 "ResponseDomain" 子选项设置，可以模拟拟似然结构的参数分布：
  • "Binomial"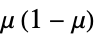0<=y<=1
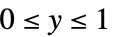
    "Gamma"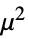
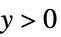
    "Gaussian"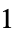
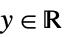
    "InverseGaussian"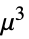
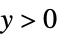
    "Poisson"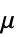
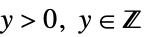
  • "Binomial" 和 "Poisson" 族的 "QuasiLikelihood" 变形可以用来建立过度散布 (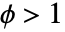) 或过低散布 (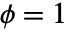) 数据模型，这区别于理论上的散布 ().
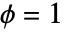  • 普通方差函数，响应域和用法包括：
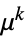
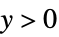
  • 电源模式、精算学、气象学等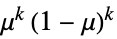
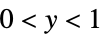
    概率模型，相关二项式等等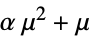
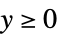
    统计模型，相关泊松等

范例

打开所有单元关闭所有单元

基本范例  (1)

一个简单线性回归模型的数据拟合：

一个标准伽玛回归模型的拟合：

一个标准逆高斯回归模型的拟合：

范围  (2)

对概率分对数模型，使用 "Binomial" 族：

对于统计数据的对数线性模型，使用 "Poisson"：

属性和关系  (3)

缺省 ExponentialFamily 和 LinkFunction 匹配 LinearModelFit：

缺省 "Binomial" 模型匹配 LogitModelFit：

拟合一个 "Gamma" 模型和类似 "QuasiLikelihood"：

模型不同于 "LogLikelihood" 中一个限制的已命名的类似模拟量：

拟合参数符合：

基于不同的对数拟似然的符合结果：

Wolfram Research (2008)，ExponentialFamily，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ExponentialFamily.html.

文本

Wolfram Research (2008)，ExponentialFamily，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ExponentialFamily.html.

CMS

Wolfram 语言. 2008. "ExponentialFamily." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialFamily.html.

APA

Wolfram 语言. (2008). ExponentialFamily. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ExponentialFamily.html 年

BibTeX

@misc{reference.wolfram_2024_exponentialfamily, author="Wolfram Research", title="{ExponentialFamily}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExponentialFamily.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_exponentialfamily, organization={Wolfram Research}, title={ExponentialFamily}, year={2008}, url={https://reference.wolfram.com/language/ref/ExponentialFamily.html}, note=[Accessed: 22-November-2024 ]}