Modulus

Modulusn

is an option that can be given in certain algebraic functions to specify that integers should be treated modulo n.

Details

  • Modulus appears as an option in Solve, Reduce, Factor, PolynomialGCD, and PolynomialLCM, as well as in linear algebra functions such as Inverse, LinearSolve, and Det.
  • Arithmetic is usually done over the full ring 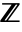of integers; setting the option Modulus specifies that arithmetic should instead be done in the finite ring .
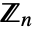  • The setting Modulus->0 specifies the full ring 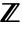of integers.
  • Some functions require that Modulus be set to a prime, or a power of a prime. 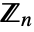is a finite field when 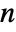is prime.
  • Equations for Modulus can be given in Eliminate and related functions.

Examples

open allclose all

Basic Examples  (1)

Solve equations:

Factor polynomials:

Compute inverse:

Scope  (6)

Compute PolynomialGCD over the integers modulo 2:

Factor a polynomial over the integers modulo 3:

Find a GroebnerBasis over the integers modulo 5:

Reduce equations over the integers modulo 7:

Compute the determinant of a matrix modulo 8:

Find a modulus for which a system of equations has a solution:

Properties & Relations  (2)

Factor a polynomial over a finite field:

Factor a polynomial over a finite Extension of rationals:

Wolfram Research (1988), Modulus, Wolfram Language function, https://reference.wolfram.com/language/ref/Modulus.html.

Text

Wolfram Research (1988), Modulus, Wolfram Language function, https://reference.wolfram.com/language/ref/Modulus.html.

CMS

Wolfram Language. 1988. "Modulus." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Modulus.html.

APA

Wolfram Language. (1988). Modulus. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Modulus.html

BibTeX

@misc{reference.wolfram_2024_modulus, author="Wolfram Research", title="{Modulus}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Modulus.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_modulus, organization={Wolfram Research}, title={Modulus}, year={1988}, url={https://reference.wolfram.com/language/ref/Modulus.html}, note=[Accessed: 22-November-2024 ]}