Factorial2 
n!!
gives the double factorial of n.
Details
- Mathematical function, suitable for both symbolic and numerical manipulation.
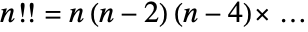 .
. - n!! is a product of even numbers for n even, and odd numbers for n odd.
- Factorial2 can be evaluated to arbitrary numerical precision.
- Factorial2 automatically threads over lists.
- Factorial2 can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (7)
Plot over a subset of the reals:
Plot over a subset of the complexes:
Series expansion at the origin:
Series expansion at Infinity:
Scope (30)
Numerical Evaluation (6)
The precision of the output tracks the precision of the input:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix Factorial2 function using MatrixFunction:
Specific Values (3)
Values of Factorial2 at fixed points:
Find the first positive maximum of Factorial2[x]:
Visualization (2)
Function Properties (10)
Real domain of the double factorial:
Double factorial has the mirror property ![]() :
:
Factorial2 threads elementwise over lists:
Factorial2 is not an analytic function:
Factorial2 is neither nondecreasing nor nonincreasing:
Factorial2 is not injective:
Factorial2 is not surjective:
Factorial2 is neither non-negative nor non-positive:
Factorial2 has both singularity and discontinuity for z≤-2:
Factorial2 is neither convex nor concave:
Differentiation (2)
Series Expansions (4)
Function Identities and Simplifications (3)
Relationship between Factorial and Factorial2 on the integers:
Generalizations & Extensions (3)
Applications (5)
Plot of the absolute value of the double factorial in the complex plane:
An infinite series for ![]() in terms of the factorial and double factorial:
in terms of the factorial and double factorial:
Calculate the first 30 digits of ![]() using this series:
using this series:
Compare with numerically evaluating Pi:
Verify an expression for the Catalan numbers in terms of double factorials:
For ![]() an odd prime, a generalization of Wilson's theorem states that
an odd prime, a generalization of Wilson's theorem states that ![]() . Verify for the first few odd primes:
. Verify for the first few odd primes:
A determinantal representation for the odd double factorials:
Properties & Relations (8)
Use FunctionExpand to express the double factorial in terms of the Gamma function:
Use FullSimplify to simplify expressions involving double factorials:
Sums involving Factorial2:
Generating function:
Recover the original power series:
Products involving the double factorial:
Factorial2 can be represented as a DifferenceRoot:
FindSequenceFunction can recognize the Factorial2 sequence:
The exponential generating function for Factorial2:
Possible Issues (3)
Neat Examples (3)
Plot Factorial2 at infinity:
Find the numbers of digits 0 through 9 in 10000!!:
Plot the ratio of doubled factorials over double factorial:
Text
Wolfram Research (1988), Factorial2, Wolfram Language function, https://reference.wolfram.com/language/ref/Factorial2.html (updated 2022).
CMS
Wolfram Language. 1988. "Factorial2." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Factorial2.html.
APA
Wolfram Language. (1988). Factorial2. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Factorial2.html