WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

Factorial
✖
Factorial

✖
n!

gives the factorial of n.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For non‐integer n, the numerical value of n! is given by Gamma[1+n].
  • For integers and half integers, Factorial automatically evaluates to exact values.
  • Factorial can be evaluated to arbitrary numerical precision.
  • Factorial automatically threads over lists.
  • Factorial can be used with Interval and CenteredInterval objects. »

Background & Context

  • Factorial represents the factorial function. In particular, Factorial[n] returns the factorial 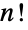of a given number 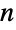, which, for positive integers, is defined as 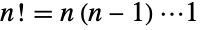. For n1,2,…, the first few values are therefore 1,2,6,24,120,720,…. The special case 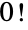is defined as 1, consistent with the combinatorial interpretation of there being exactly one way to arrange zero objects. For a general complex number 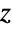, z!=TemplateBox[{{z, +, 1}}, Gamma], where the Gamma function TemplateBox[{z}, Gamma] is defined by TemplateBox[{z}, Gamma]=int_0^inftyⅇ^(-t) t^(z-1)dt for all complex values of 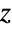except when 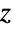is a negative integer (in which case 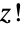is complex infinity). Factorials of half integers are given by rational multiples of .
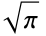  • Factorials are best known for counting fixed orderings of the elements of a list, known as permutations, which can be generated using Permutations. There are 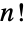permutations of a list of 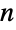(distinct) elements, a fact that follows from there being 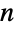spots to place the first element, 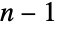spots to place the second element once the first is placed, 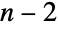spots to place the third element once the first two elements are placed and so on until a single spot remains in which to place the last element. There are therefore 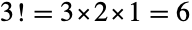permutations of 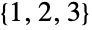, namely 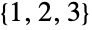, , 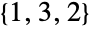, , 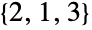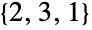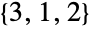and .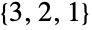
  • More generally, for an 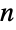-element multiset having 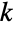distinct elements with 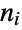copies of the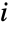 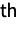^(th) distinct element (so 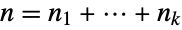), the number of permutations equals the multinomial coefficient 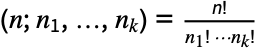, given by Multinomial. The multinomial coefficient 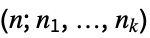(n;n_1,...,n_(k)) also counts the ways to partition an 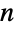-element set into 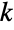labeled subsets of sizes n1,…,nk. Hence the binomial coefficient TemplateBox[{n, m}, Binomial], given by Binomial and defined to count the 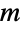-element subsets of an 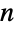-element set, satisfies TemplateBox[{n, m}, Binomial]=(n;m,n-m)=(n!)/(m! (n-m)!).
  • The factorial function satisfies the recurrences 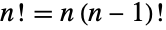and 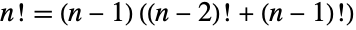. It grows faster than any exponential function, as shown by Stirling's approximation 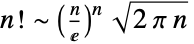. Factorials also appear in fundamental results in number theory and analysis. Wilson's theorem states that TemplateBox[{{{{(, {n, -, 1}, )}, !}, =, {-, 1}}, n}, Mod] if and only if 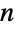is prime. If 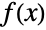is an infinitely differentiable scalar function, then its Taylor series representation about a point 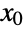(computable using Series) is given by 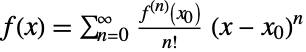. Setting 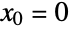and 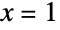in the Taylor series of the exponential function 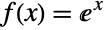yields the beautiful identity for E (the base of the natural logarithm) .
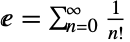  • Other functions associated with or generalizing Factorial include Factorial2, FactorialPower, TemplateBox[{Subfactorial, paclet:ref/Subfactorial}, RefLink, BaseStyle -> {InlineFormula}], QFactorial, BarnesG and Pochhammer.

Examples

open allclose all

Basic Examples  (7)Summary of the most common use cases

Compute the factorial for the first few integers:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-bx2b22
Out[1]=1
In[3]:=3
✖
https://wolfram.com/xid/0lddmma-e2pfyq
Out[3]=3

Evaluate at real values:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-1tb0k
Out[1]=1

Plot over a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gi13sj
Out[1]=1

Plot over a subset of the complexes:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-kiedlx
Out[1]=1

Series expansion at the origin:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ej957w
Out[1]=1

Series expansion at Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-cugjvu
Out[1]=1

Series expansion at a singular point:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ii6s9p
Out[1]=1

Scope  (34)Survey of the scope of standard use cases

Numerical Evaluation  (6)

Evaluate numerically:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-l274ju
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-whe1w
Out[2]=2

Evaluate to high precision:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-b0wt9
Out[1]=1

The precision of the output tracks the precision of the input:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-y7k4a
Out[2]=2

Complex number inputs:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-hfml09
Out[1]=1

Evaluate efficiently at high precision:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-bq2c6r
Out[2]=2

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gnclzo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-dtvr5v
Out[2]=2

Or compute average-case statistical intervals using Around:

In[3]:=3
✖
https://wolfram.com/xid/0lddmma-cw18bq
Out[3]=3

Compute the elementwise values of an array:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-thgd2
Out[1]=1

Or compute the matrix Factorial function using MatrixFunction:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-o5jpo
Out[2]=2

Specific Values  (5)

Values of Factorial at fixed points:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-nww7l
Out[1]=1

Values at zero:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-e41pf2
Out[1]=1

Evaluate for large arguments:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gxbgq
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-cndv4n
Out[2]=2

Evaluate for half-integer arguments:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-c6yk4v
Out[1]=1

Find the positive minimum of Factorial[x]:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-f2hrld
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-cj5txq
Out[2]=2

Visualization  (2)

Plot the Factorial function:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ecj8m7
Out[1]=1

Plot the real part of :

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ouu484
Out[1]=1

Plot the imaginary part of :

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-fz1xl5
Out[2]=2

Function Properties  (10)

Real domain of the factorial:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-cl7ele
Out[1]=1

Complex domain:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-de3irc
Out[2]=2

Factorial threads elementwise over lists:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-c3oe4
Out[1]=1

The factorial has the mirror property :

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-heoddu
Out[1]=1

Factorial is not an analytic function:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gva6yl
Out[1]=1

However, it is a meromorphic function in the complex plane:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-vflufa
Out[2]=2

Factorial is neither nondecreasing nor nonincreasing:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-2ra8g
Out[1]=1

Factorial is not injective:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-c9npzh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-b5buvp
Out[2]=2

Factorial is not surjective:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-patce
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-bcrbvs
Out[2]=2

Factorial is neither non-negative nor non-positive:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-dvzykj
Out[1]=1

Factorial has both singularity and discontinuity for negative integers:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-fyfbxx
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-5vh4e
Out[2]=2

Factorial is neither convex nor concave:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-l0srvu
Out[1]=1

Differentiation  (2)

First derivative with respect to z:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-krpoah
Out[1]=1

Higher derivatives with respect to z:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-z33jv
Out[1]=1

Plot the higher derivatives with respect to z:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-fxwmfc
Out[2]=2

Series Expansions  (5)

Find the Taylor expansion using Series:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ewr1h8
Out[1]=1

Plots of the first three approximations around :

In[3]:=3
✖
https://wolfram.com/xid/0lddmma-binhar
Out[4]=4

Find the series expansion at Infinity (Stirling's approximation):

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-syq
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-b5vva5
Out[2]=2

Series at :

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-bf2qwg
Out[1]=1

Find series expansion for an arbitrary symbolic direction :

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-t5t
Out[1]=1

Taylor expansion at a generic point:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-jwxla7
Out[1]=1

Recurrence Identities and Simplifications  (2)

Recurrence relations:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-fe2syb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0lddmma-t71ed
Out[3]=3

For positive integers (n-1)! = TemplateBox[{n}, Gamma]:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-lxi8j
Out[1]=1

Function Representations  (2)

Integral representation of the factorial function:

In[8]:=8
✖
https://wolfram.com/xid/0lddmma-kgkzwa
Out[8]=8

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ppzpg3

Generalizations & Extensions  (4)Generalized and extended use cases

Evaluate to high precision:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-mn7jd8
Out[1]=1

The precision of the output tracks the precision of the input:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-b40evc
Out[1]=1

Infinite arguments give symbolic results:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma
Out[2]=2

Factorial allows derivatives:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-ensplw
Out[1]=1

Applications  (6)Sample problems that can be solved with this function

Make a table of half-integer factorials:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-f8vy62
Out[1]=1

Number of permutations of 6 elements:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma
Out[2]=2

Plot of the absolute value of Factorial in the complex plane:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-fnm8z0
Out[1]=1

Find the asymptotic expansion of ratios of factorials:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1

Volume of an n‐dimensional unit hypersphere:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1

Low‐dimensional cases:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma
Out[2]=2

Plot the volume of the unit hypersphere as a function of dimension:

In[3]:=3
✖
https://wolfram.com/xid/0lddmma
Out[3]=3

Find the series expansion at -∞:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-bsrx9a
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-kyip1d
Out[2]=2

Properties & Relations  (9)Properties of the function, and connections to other functions

Use FullSimplify to simplify expressions involving Factorial:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-eezh32
Out[1]=1

Compute a generating function sum involving Factorial:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gqn7vx
Out[1]=1

Compute numerical sums involving Factorial:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma
Out[2]=2

The generating function is divergent:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-vlcl6
Out[1]=1

Use regularization to obtain a closed-form generating function:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-dltyxn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0lddmma-c6fcia
Out[3]=3

Generating function as a formal series:

In[4]:=4
✖
https://wolfram.com/xid/0lddmma-b2m5tf
Out[4]=4

Some integrals can be done:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-b3ros8
Out[1]=1

Product of factorials:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-dwxqsh
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-flehi8
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0lddmma-i6cllf
Out[3]=3

Factorial can be represented as a DifferenceRoot:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-pxkma
Out[1]=1

FindSequenceFunction can recognize the Factorial sequence:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-hj2mn6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma-5okec
Out[2]=2

The exponential generating function for Factorial:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-gaiyeu
Out[1]=1

Possible Issues  (2)Common pitfalls and unexpected behavior

Large arguments can give results too large to be computed explicitly, even approximately:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-b18m9u
Out[1]=1

Smaller values work:

In[2]:=2
✖
https://wolfram.com/xid/0lddmma-bqnowb
Out[2]=2

Machine-number inputs can give high‐precision results:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0lddmma
Out[2]=2

Neat Examples  (3)Surprising or curious use cases

In[1]:=1
✖
https://wolfram.com/xid/0lddmma-j4hze
Out[1]=1

Nested factorials over the complex plane:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1

Plot Factorial at infinity:

In[1]:=1
✖
https://wolfram.com/xid/0lddmma
Out[1]=1
Wolfram Research (1988), Factorial, Wolfram Language function, https://reference.wolfram.com/language/ref/Factorial.html (updated 2022).
✖
Wolfram Research (1988), Factorial, Wolfram Language function, https://reference.wolfram.com/language/ref/Factorial.html (updated 2022).

Text

Wolfram Research (1988), Factorial, Wolfram Language function, https://reference.wolfram.com/language/ref/Factorial.html (updated 2022).

✖
Wolfram Research (1988), Factorial, Wolfram Language function, https://reference.wolfram.com/language/ref/Factorial.html (updated 2022).

CMS

Wolfram Language. 1988. "Factorial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Factorial.html.

✖
Wolfram Language. 1988. "Factorial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/Factorial.html.

APA

Wolfram Language. (1988). Factorial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Factorial.html

✖
Wolfram Language. (1988). Factorial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Factorial.html

BibTeX

@misc{reference.wolfram_2025_factorial, author="Wolfram Research", title="{Factorial}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Factorial.html}", note=[Accessed: 24-May-2025 ]}

✖
@misc{reference.wolfram_2025_factorial, author="Wolfram Research", title="{Factorial}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/Factorial.html}", note=[Accessed: 24-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_factorial, organization={Wolfram Research}, title={Factorial}, year={2022}, url={https://reference.wolfram.com/language/ref/Factorial.html}, note=[Accessed: 24-May-2025 ]}

✖
@online{reference.wolfram_2025_factorial, organization={Wolfram Research}, title={Factorial}, year={2022}, url={https://reference.wolfram.com/language/ref/Factorial.html}, note=[Accessed: 24-May-2025 ]}