FindFormula

FindFormula[data]

data を近似する純関数を求める．

FindFormula[data,x]

data を近似する変数 x の記号関数を求める．

FindFormula[data,x,n]

data を近似する関数を n 個まで求める．

FindFormula[data,x,n,prop]

特性 prop に関連付けられた最適関数を n 個まで返す．

FindFormula[data,x,n,{prop1,prop2,…}]

特性 prop1，prop2等と関連付けられた最適関数を n 個まで返す．

詳細とオプション

  • データは{{x1,y1},{x2,y2},…}または{{1,y1},{2,y2},…}の形式の配列，あるいはTimeSeriesオブジェクトでなければならない．
  • {y1,y2,…}形式のデータは{{1,y1},{2,y2},…}形式のデータに等しい．
  • FindFormula[data,x,n,All]は可能なすべての特性を持つDatasetオブジェクトを作る．
  • サポートされる特性
  • "Score"内部スコア
    "Complexity"関数の複雑さ
    "Error"平均二乗誤差
    All上記の特性すべて
  • 使用可能なオプション
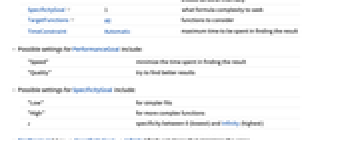
  • PerformanceGoal Automaticパフォーマンスのどの面について最適化するか
    RandomSeeding Automatic内部的にどの擬似乱数生成器のシードを使うか
    SpecificityGoal 1どのような複雑さの形式を求めるか
    TargetFunctions All考慮する関数
    TimeConstraintAutomatic結果を求めるまでの最大時間
  • PerformanceGoalの可能な設定
  • "Speed"結果を求めるまでの時間を最短にする
    "Quality"よりよい結果を求めようとする
  • SpecificityGoalの可能な設定
  • "Low"より簡単なフィット
    "High"より複雑な関数
    s0（最低）からInfinity（最高）までの特定性
  • FindFormula[data,x,SpecificityGoal->Infinity]は誤差を最小にする解を求める．
  • 1に等しいSpecificityGoalは，最高の予測パフォーマンスを与える．
  • TargetFunctionsの可能な設定
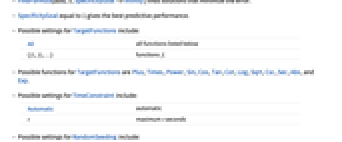
  • All以下にリストされたすべての関数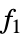
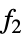    {f_(1),f_(2),…}関数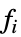
  • TargetFunctionsの可能な関数には，Plus，Times，Power，Sin，Cos，Tan，Cot，Log，Sqrt，Csc，Sec，Abs，Expがある．
  • TimeConstraintの可能な設定
  • Automatic自動
    t最大 t 秒
  • RandomSeedingの可能な設定
  • Automatic関数が呼ばれるたびに自動的にシードし直す
    Inherited内部的にシードされた乱数を使う
    seed明示的な整数または数列をシードとして使う

例題

すべて開くすべて閉じる

例  (2)

関数 x Sin[x]の値の表を作る：

FindFormulaはデータを生成する式を求める：

既知のメルセンヌ(Mersenne)素数の指数をプロットする：

データを説明する最も単純な関数を求める：

フィットした関数をデータとともに可視化する：

スコープ  (3)

正規分布に従うノイズのあるデータを生成する：

データを可視化する：

データを近似する最初の5つの最良関数を求める：

フィットされた関数をデータとともに可視化する：

正規分布に従うノイズのあるデータを生成する：

データを可視化する：

データを近似する最初の5つの関数について，データ集合を可視化する：

正規分布に従うノイズのあるデータを生成する：

データを可視化する：

最初の300のフィットを見，そのスコアをSpecificityGoalのさまざまな設定についての誤差と複雑さの関数としてプロットする：

データにフィットした最初の関数を可視化する：

オプション  (4)

PerformanceGoal  (1)

正規分布に従うノイズのあるデータを生成する：

データを可視化する：

データをその内部スコアとともに近似する最良関数を求める：

PerformanceGoalを使ってその内部スコアとともにデータを近似する最良関数を求める：

フィットされた関数をデータとともに可視化する：

RandomSeeding  (1)

一様分布に従うノイズでデータを生成する：

FindFormulaのいろいろな評価を比較し，その違いを見る：

オプションRandomSeedingを使って異なる結果にならないようにする：

SpecificityGoal  (1)

正規分布に従うノイズのあるデータを生成する：

データを可視化する：

SpecificityGoalのさまざまな値を使ってエラーのあるデータを近似する最良関数を求める：

フィットした関数をデータとともに可視化する：

TargetFunctions  (1)

正規分布に従うノイズを持つデータを生成する：

データを可視化する：

データを近似する最良関数を求める：

TargetFunctionsを使ってデータを近似する最良関数を求める：

フィットされた関数をデータとともに可視化する：

アプリケーション  (3)

人口増加  (1)

ポーランドの人口増加：

データを説明する最良の関数を求める：

フィットした関数をデータとともに可視化する：

最初の100個の素数のフィットを求める：

フィットをデータおよび次の200個の素数と比較する：

微分方程式  (1)

微分方程式の数値解についてのフィットを求める：

フィットとデータを比較する：

軌道力学  (1)

惑星の軌道周期と半長軸をプロットする：

軌道周期から軌道半径を説明する最も簡単な関数を求める：

比例定数を求める：

ケプラー(Kepler)の第3法則によって与えられる厳密な式と比較する：

比例の厳密な定数には値がある：

軌道データから得たさまざまな値と直接比較する：

Wolfram Research (2015), FindFormula, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindFormula.html （2017年に更新）.

テキスト

Wolfram Research (2015), FindFormula, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindFormula.html （2017年に更新）.

CMS

Wolfram Language. 2015. "FindFormula." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/FindFormula.html.

APA

Wolfram Language. (2015). FindFormula. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindFormula.html

BibTeX

@misc{reference.wolfram_2024_findformula, author="Wolfram Research", title="{FindFormula}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/FindFormula.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findformula, organization={Wolfram Research}, title={FindFormula}, year={2017}, url={https://reference.wolfram.com/language/ref/FindFormula.html}, note=[Accessed: 22-November-2024 ]}