FindShortestTour

FindShortestTour[{v1,v2,…}]

attempts to find an ordering of the vi that minimizes the total distance on a tour that visits all the vi once.

FindShortestTour[graph]

attempts to find an ordering of the vertices in graph that minimizes the total length when visiting each vertex once.

FindShortestTour[{v1,v2,…},j,k]

finds an ordering of the vi that minimizes the total distance on a path from vj to vk.

FindShortestTour[graph,s,t]

finds an ordering of the vertices that minimizes the total length on a path from s to t.

FindShortestTour[{vw,…},…]

uses rules vw to specify the graph g.

FindShortestTour[dataprop,…]

gives the property prop for data.

Details and Options

  • FindShortestTour is also known as the traveling salesman problem (TSP).
  • FindShortestTour returns a list of the form {dmin,{vi1,vi2,…}}, where dmin is the length of the tour found, and {vi1,vi2,…} is the ordering.
  • In FindShortestTour[dataprop,…], possible forms for prop include:
  • "Elements"the element of the shortest tour
    "Indices"the indices of the shortest tour
    "Length"the distance of the shortest tour
    {prop1,prop2,…}a list of multiple forms
    Allan association giving element, index and distance
  • The following options can be given:
  • DistanceFunction Automaticfunction to apply to pairs of objects
    MethodAutomaticmethod to use
  • Automatic settings for DistanceFunction depending on the vi include:
  • EuclideanDistancenumbers of lists of numbers
    EditDistancestrings
    GeoDistancegeo positions
  • For graph, the distance is taken to be GraphDistance, which is the shortest path length for an unweighted graph and the sum of weights for a weighted graph.

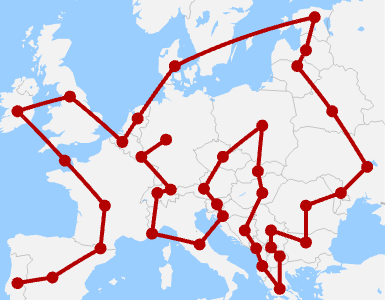
Examples

open allclose all

Basic Examples  (3)

Find the length and ordering of the shortest tour through points in the plane:

Order the points according to the tour found:

Plot the tour:

Find the shortest tour in a graph:

Highlight the tour:

Find a shortest tour of Europe from Albania to Spain:

Show the tour:

Scope  (7)

FindShortestTour works with a list of points:

A list of strings:

A list of geodetic positions:

Undirected graphs:

Weighted graphs:

Use rules to specify the graph:

FindShortestTour works with large graphs:

Options  (3)

DistanceFunction  (3)

By default, EditDistance is used for strings:

This finds the shortest tour through 100 points, with a penalty added to cross a "river":

This plots the tour with the "river" in red:

This defines a sparse distance matrix among six points and finds the shortest tour:

This plots the shortest tour in red, and the distance on each edge:

Applications  (3)

Find the shortest tour visiting random points in the plane:

Show the tour:

The shortest tour visiting random points in 3D:

Find a traveling salesman tour of Europe:

Latitude and longitude of geographical centers:

Show the tour:

Draw Leonardo da Vinci’s Mona Lisa as a continuous-line drawing:

Convert the image to points:

Draw Mona Lisa:

Properties & Relations  (2)

FindShortestTour gives an empty list for non-Hamiltonian graphs:

A graph with no shortest tour may have a shortest path visiting every vertex:

Possible Issues  (2)

For large datasets, FindShortestTour finds a tour whose length is at least close to the minimum:

Use PerformanceGoal->"Quality" to find an optimal result:

In FindShortestTour, rules are taken to be undirected edges:

Neat Examples  (1)

Plan a tour through every country of the world:

Use an azimuthal projection to visualize the tour:

Visualize the tour on a spherical Earth:

Wolfram Research (2007), FindShortestTour, Wolfram Language function, https://reference.wolfram.com/language/ref/FindShortestTour.html (updated 2024).

Text

Wolfram Research (2007), FindShortestTour, Wolfram Language function, https://reference.wolfram.com/language/ref/FindShortestTour.html (updated 2024).

CMS

Wolfram Language. 2007. "FindShortestTour." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FindShortestTour.html.

APA

Wolfram Language. (2007). FindShortestTour. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindShortestTour.html

BibTeX

@misc{reference.wolfram_2024_findshortesttour, author="Wolfram Research", title="{FindShortestTour}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FindShortestTour.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findshortesttour, organization={Wolfram Research}, title={FindShortestTour}, year={2024}, url={https://reference.wolfram.com/language/ref/FindShortestTour.html}, note=[Accessed: 18-November-2024 ]}