FindShortestTour

FindShortestTour[{v1,v2,…}]

すべての viを1回ずつ訪れる場合の総距離を最小化するような viの順序を求めようとする．

FindShortestTour[graph]

各頂点を1回訪れる場合に全長を最短にする graph 中の頂点の順序を求めようとする．

FindShortestTour[{v1,v2,…},j,k]

vjから vkまでの経路の総距離を最短にする viの順序を求める．

FindShortestTour[graph,s,t]

s から t までの総延長を最短にする頂点の順序を求める．

FindShortestTour[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

FindShortestTour[dataprop,…]

data の特性 prop を与える．

詳細とオプション

  • FindShortestTourは，巡回セールスマン問題(TSP)としても知られている．
  • FindShortestTourは{dmin,{vi1,vi2,…}}の形式のリストを返す．dminは求まったコースの長さ，{vi1,vi2,…}はその順序である．
  • 以下は，FindShortestTour[dataprop,…]における prop の可能な形である．
  • "Elements"最短ツアーの要素
    "Indices"最短ツアーの指標
    "Length"最短ツアーの距離
    {prop1,prop2,…}複数の形式のリスト
    All要素，指標，距離を与える連想
  • 次は，可能なオプションである．
  • DistanceFunction Automaticオブジェクトのペアに適用する関数
    MethodAutomatic使用するメソッド
  • viに依存するDistanceFunctionの自動設定には以下がある．
  • EuclideanDistance数のリストの数
    EditDistance文字列
    GeoDistance地理的位置
  • graph については，距離はGraphDistanceであるとみなされる．これは，重みのないグラフについては最短距離の長さ，重み付きグラフについては重みの総和である．

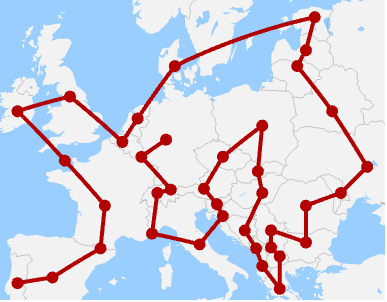
例題

すべて開くすべて閉じる

例  (3)

平面上の点を通る最短距離の長さとその順序を求める：

求まったコースに沿って点を並べる：

コースをプロットする：

グラフ中の最短コース求める：

コースをハイライトする：

ヨーロッパのアルバニアからスペインまでの最短順路を求める：

順路を示す：

スコープ  (7)

FindShortestTourは，点のリストに使うことができる：

文字列のリスト：

測地位置のリスト：

無向グラフ：

重み付きグラフ：

規則を使ってグラフを指定する：

FindShortestTourは大きいグラフに使うことができる：

オプション  (3)

DistanceFunction  (3)

デフォルトで，EditDistanceは文字列に使われる：

「川」を渡る際にペナルティが設けられた，100個の点を通る最短コースを求める：

次はコースのプロットで「川」が赤で示されている：

6個の点の間の疎な距離行列を定義し，最短コースを求める：

最短コース（赤）だけでなく各辺の距離もプロットする：

アプリケーション  (3)

平面上の点をランダムに訪れる最短コースを求める：

コースを示す：

3Dのランダムな点を訪れる最短コース：

巡回セールスマンのヨーロッパツアーのコースを求める：

地理的中心の経緯度：

コースを示す：

レオナルド・ダ・ヴィンチの「モナリザ」を連続する線で描く：

画像を点に変換する：

「モナリザ」を描く：

特性と関係  (2)

FindShortestTourは，ハミルトングラフではないものに対しては空リストを与える：

最短順路がないグラフにも各頂点を訪れる最短経路があることがある：

考えられる問題  (2)

大きいデータ集合については，FindShortestTourは長さが少なくとも最短に近い順路を求める：

PerformanceGoal->"Quality"を使って最適な結果を求める：

FindShortestTourでは，規則は無向辺であるとみなされる：

おもしろい例題  (1)

世界中のすべての国を回るツアーを計画する：

方位図法を用いてツアーを可視化する：

球体の地球上でツアーを可視化する：

Wolfram Research (2007), FindShortestTour, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindShortestTour.html （2024年に更新）.

テキスト

Wolfram Research (2007), FindShortestTour, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindShortestTour.html （2024年に更新）.

CMS

Wolfram Language. 2007. "FindShortestTour." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FindShortestTour.html.

APA

Wolfram Language. (2007). FindShortestTour. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindShortestTour.html

BibTeX

@misc{reference.wolfram_2024_findshortesttour, author="Wolfram Research", title="{FindShortestTour}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FindShortestTour.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findshortesttour, organization={Wolfram Research}, title={FindShortestTour}, year={2024}, url={https://reference.wolfram.com/language/ref/FindShortestTour.html}, note=[Accessed: 18-November-2024 ]}