Floor 
詳細

- 記号操作・数値操作の両方に適した数学関数である.
- Floor[x]はStandardFormやInputForm内で,⌊x⌋や
 lf
lf
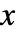
 rf
rf あるいは\[LeftFloor]x \[RightFloor]という形で入力できる. »
あるいは\[LeftFloor]x \[RightFloor]という形で入力できる. » - Floor[x]は,
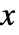 が任意の数値である場合整数を返す.この際,x が明示的な数値であるかないかにかかわらない. »
が任意の数値である場合整数を返す.この際,x が明示的な数値であるかないかにかかわらない. » - Floor[x]は複素数の実部と虚部に別々に適用される.
- a が正の実数でなければ,Floor[x,a]は式Floor[x,a]a Floor[x/a]によって定義される. »
- 厳密な数値に対して,Floorは結果を見出すために数値近似を行う.この手続きは,大域変数$MaxExtraPrecisionの設定により影響を受ける.
- Floorは自動的にリストに縫い込まれる. »
例題
すべて開く すべて閉じる例 (4)
スコープ (30)
数値評価 (7)
1引数のFloorは常に厳密な結果を返す:
Floorは実数値区間を扱うことができる:
Aroundを使って平均的な場合の統計区間を計算する:
MatrixFunctionを使って行列のFloor関数を計算することもできる:
関数の特性 (9)
微分と積分 (4)
特性と関係 (12)
おもしろい例題 (3)
関連項目
Ceiling Round IntegerPart Chop Piecewise BinCounts Quantile FindDivisions
Function Repository: MinMaxRounded
テクニカルノート
-
▪
- 数値操作関数 ▪
- 区分関数 ▪
- 演算子 ▪
- 実装に関するノート: 数値および関連関数
関連するガイド
-
▪
- 数値関数 ▪
- GPU計算 ▪
- 数学関数 ▪
- NVIDIAを使ったGPU計算 ▪
- 条件文 ▪
- 統計学で使用される関数 ▪
- 数の表現
履歴
1988 で導入 (1.0) | 1996 で更新 (3.0) ▪ 2007 (6.0)
テキスト
Wolfram Research (1988), Floor, Wolfram言語関数, https://reference.wolfram.com/language/ref/Floor.html (2007年に更新).
CMS
Wolfram Language. 1988. "Floor." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Floor.html.
APA
Wolfram Language. (1988). Floor. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Floor.html
BibTeX
@misc{reference.wolfram_2025_floor, author="Wolfram Research", title="{Floor}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Floor.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_floor, organization={Wolfram Research}, title={Floor}, year={2007}, url={https://reference.wolfram.com/language/ref/Floor.html}, note=[Accessed: 07-February-2026]}

