Floor 
更多信息

- 数学函数,适宜于符号和数值计算.
- 可以用 ⌊x⌋、
 lf
lf
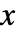
 rf
rf 或
或
\[LeftFloor]x \[RightFloor] 以 StandardForm 和 InputForm 输入 Floor[x]. » 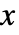 是任意数值型量 (numeric quantity) 时,Floor[x] 返回一个整数,不管它是否是一个明确的数字. »
是任意数值型量 (numeric quantity) 时,Floor[x] 返回一个整数,不管它是否是一个明确的数字. »- Floor[x] 分别作用于复数的实部和虚部.
- 如果 a 不是正实数,Floor[x,a] 由公式 Floor[x,a]a Floor[x/a] 定义. »
- 对于精确的数值型量,Floor 内部使用数值近似得到结果. 全局变量 $MaxExtraPrecision 的设置可能影响计算过程.
- Floor 自动逐项作用于列表的各个元素. »
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (30)
数值计算 (7)
函数的属性 (9)
微分与积分 (4)
属性和关系 (12)
巧妙范例 (3)
Wolfram Research (1988),Floor,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Floor.html (更新于 2007 年).
文本
Wolfram Research (1988),Floor,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Floor.html (更新于 2007 年).
CMS
Wolfram 语言. 1988. "Floor." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2007. https://reference.wolfram.com/language/ref/Floor.html.
APA
Wolfram 语言. (1988). Floor. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Floor.html 年