FluidFlowPDEComponent
FluidFlowPDEComponent[vars,pars]
生成带有变量 vars 和参数 pars 的流偏微分方程项.
更多信息




- FluidFlowPDEComponent 返回用作偏微分方程一部分的微分算子之和:
- FluidFlowPDEComponent 模拟粘性流体在外加力和约束条件下的流流动.
- FluidFlowPDEComponent 创建偏微分方程分量以进行稳态、时间相关的参数分析.
- FluidFlowPDEComponent 模拟流体流动现象,速度
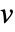 、
、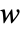 和
和 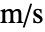 以 [
以 [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/6.png) ] 为单位,
] 为单位,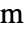 为自变量,单位为 [
为自变量,单位为 [![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/8.png) ],时间变量
],时间变量 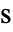 单位为 [
单位为 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/10.png) ].
]. - FluidFlowPDEComponent 创建二维和三维空间中的偏微分方程分量.
- 静态变量 vars 为 vars={{u[x1,…,xn],v[x1,…,xn],…,p[x1,…,xn]},{x1,…,xn}}.
- 时间相关变量或本征模变量 vars 为 vars={{u[t,x1,…,xn],v[t,x1,…,xn],…,p[x1,…,xn]},t,{x1,…,xn}}.
- FluidFlowPDEComponent 生成的不同分析类型的方程取决于 vars 的形式.
- FluidFlowPDEComponent 使用向量值的纳维-斯托克斯方程与连续性方程相结合创建方程组.
- 流体动力学偏微分方程 FluidFlowPDEComponent 的时变平衡方程基于纳维-斯托克斯方程和连续性方程,其中
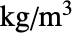 为质量密度,单位为 [
为质量密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/12.png) ],
],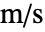 为流体速度,单位为 [
为流体速度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/14.png) ],
],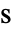 为时间,单位为 [
为时间,单位为 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/16.png) ],
],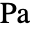 为粘性应力张量,单位为 [
为粘性应力张量,单位为 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/18.png) ],
],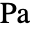 为压强,单位为 [
为压强,单位为 [![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/20.png) ],
],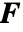 为单位矩阵,
为单位矩阵,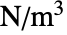 为体积负荷矢量,单位为 [
为体积负荷矢量,单位为 [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/23.png) ]:
]: - 在可压缩形式中,粘性应力张量
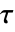 给定为:
给定为: - 在这里,
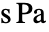 [
[![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/28.png) ] 是动力黏度,而无限小、微小变形应变率测量
] 是动力黏度,而无限小、微小变形应变率测量 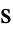 [1/
[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/30.png) ]给定为:
]给定为: - FluidFlowPDEComponent 根据质量密度
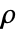 值的性质,创建可压缩或不可压缩流体流动的偏微分方程模型.
值的性质,创建可压缩或不可压缩流体流动的偏微分方程模型. - 可压缩流体动力学模型给出如下:
- 对于恒定的质量密度值
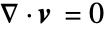 ,质量连续方程简化为体积连续方程
,质量连续方程简化为体积连续方程 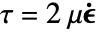 ,粘性应力张量随之简化为
,粘性应力张量随之简化为 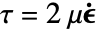 .
. - 不可压缩流体动力学模型给出如下:
- 稳态平衡方程有
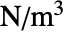 .
. - 纳维-斯托克斯模型的项是力密度,单位为 [
![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/39.png) ].
]. - 质量连续方程模型项的单位涉及力密度,单位为 [
![TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/(", , {"m", ^, 3}, , "s", , ")"}, kilograms per meter cubed second, {{(, "Kilograms", )}, /, {(, {{"Meters", ^, 3}, , "Seconds"}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/40.png) ],而体积连续方程的单位为[1/
],而体积连续方程的单位为[1/![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/41.png) ].
]. - 层流流动通常出现在
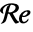 的情况下,其中
的情况下,其中 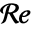 是雷诺数.
是雷诺数. - 雷诺数
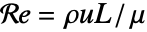 的定义为
的定义为 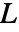 ,其中
,其中 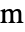 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/47.png) ] 是特征长度,
] 是特征长度,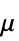 是流速.
是流速. - 可以给出以下参数 pars:
-
参数 默认值 符号 "DynamicViscosity" - 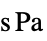 ,动力粘度,单位为 [
,动力粘度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"s", , "Pa"}, second pascals, {"Pascals", , "Seconds"}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/50.png) ]
]
"FluidLoad" 0 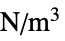 ,体积力密度,单位为 [
,体积力密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/52.png) ]
]
"FluidDynamicsMaterialModel" "Newtonian" 无 "MassDensity" - 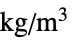 ,密度,单位为 [
,密度,单位为 [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/FluidFlowPDEComponent.zh/54.png) ]
]
"Material" - 无 "ModelForm" "Conservative" 无 "ReynoldsNumber" - 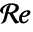
- 如果 "Material" 已指定了,则材料常数将从材料数据中提取;否则,需要指定相关的材料参数.
- 可以指定雷诺数
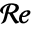 ,而不是材料参数:
,而不是材料参数: - 默认的材料模型是牛顿流动模型.
- 可以通过在参数 pars 中设置 "FluidDynamicsMaterialModel" 键来指定替代的材料模型.
- 以下是可用的非牛顿材料模型:
-
材料模型名称 "PowerLaw" "Carreau" "Bingham-Papanastasiou" "Herschel-Bulkley-Papanastasiou" - 对于可压缩的非牛顿流体,粘性应力张量
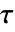 的定义如下:
的定义如下: - 表观粘度
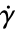 是剪切速率
是剪切速率 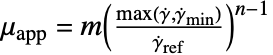 的函数.
的函数. - 可以通过 "FluidDynamicsMaterialModel"-><"ModelName"-><...>> 来指定具有 "ModelName" 的材料模型的附加材料模型特定参数.
- "PowerLaw" 模型,作为一个通用模型,实现了
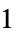 .
. - 可以为 "PowerLaw" 模型给出以下参数:
-
参数 默认值 符号 "PowerLawExponent" 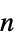
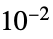 ,指数
,指数
"MinimalShearRate" 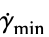
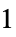 ,最小剪切速率
,最小剪切速率"ReferenceShearRate" 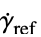
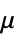 ,参考剪切速率
,参考剪切速率"PowerLawViscosity" 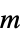
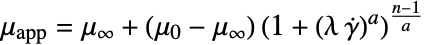 ,幂律粘度
,幂律粘度 - 通用的 "Carreau" 模型适用于聚合物或血液流动,实现了
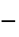 .
. - "Carreau" 模型可以设置以下参数:
-
参数 默认值 符号 "PowerLawExponent" 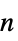
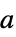 ,指数
,指数
"TransitionExponent" 2 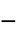 ,指数
,指数"InfiniteShearRateViscosity" 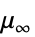
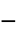 ,无限剪切速率下的粘度
,无限剪切速率下的粘度"Lambda" 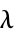
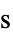 ,松弛时间,单位为 [
,松弛时间,单位为 [![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/FluidFlowPDEComponent.zh/79.png) ]
]"ZeroShearRateViscosity" 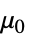
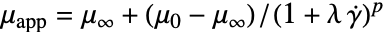 ,零剪切速率下的粘度
,零剪切速率下的粘度 - "Carreau" 模型也可用于 Cross 模型,其中
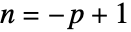 ,且
,且 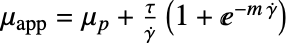 .
. - "Bingham-Papanastasiou" 模型适用于粘塑性材料,实现了
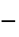 .
. - "Bingham-Papanastasiou" 模型可以设置以下参数:
-
参数 默认值 符号 "PlasticViscosity" 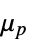
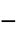 ,塑性粘度
,塑性粘度
"YieldStress" 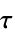
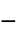 ,屈服应力
,屈服应力"ShearRateFactor" 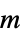
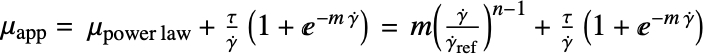 ,剪切速率因子
,剪切速率因子 - "Herschel-Bulkley-Papanastasiou" 模型,"PowerLaw" 与 "Bingham-Papanastasiou" 模型的混合,实现了
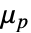 . 该模型使用幂律计算 Bingham–Papanastasiou 模型的塑性粘度
. 该模型使用幂律计算 Bingham–Papanastasiou 模型的塑性粘度 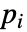 ,并且可以设置两个模型的参数.
,并且可以设置两个模型的参数. - 自定义表观粘度函数 fun 可以指定为 "FluidDynamicsMaterialModel"-><"Custom"-><"ApparentViscosityFunction"->fun>>.
- 自定义表观粘度函数 fun 的函数签名是 fun[name_,vars_,pars_,data__].
- 自定义粘性应力张量函数 fun 可以指定为 "FluidDynamicsMaterialModel"->fun.
- 自定义粘性应力张量函数 fun 的函数签名是 fun[vars_,pars_,data__].
- 非等温流动可以通过 Boussinesq 近似来建模.
- FluidFlowPDEComponent 使用 "SIBase" 单位. 几何图形必须采用与偏微分方程相同的单位.
- 如果 FluidFlowPDEComponent 取决于在关联 pars 中指定为 …,keypi…,pivi,…] 的参数
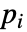 ,则参数
,则参数 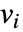 将替换为
将替换为 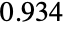 .
.
范例
打开所有单元关闭所有单元范围 (8)
用 Activate 激活一个特定材料的流偏微分方程模型:
指定二维符号稳态流体动力学偏微分方程,其中动态粘度为 ![]() ,质量密度为
,质量密度为 ![]() :
:
指定三维符号稳态流体动力学偏微分方程,其中动态粘度为 ![]() ,质量密度为
,质量密度为 ![]() :
:
指定二维符号式时间相关的流体动力学偏微分方程,其中动态粘度为 ![]() ,质量密度为
,质量密度为 ![]() :
:
应用 (3)
非牛顿流体 (1)
Wolfram Research (2024),FluidFlowPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html (更新于 2024 年).
文本
Wolfram Research (2024),FluidFlowPDEComponent,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html (更新于 2024 年).
CMS
Wolfram 语言. 2024. "FluidFlowPDEComponent." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html.
APA
Wolfram 语言. (2024). FluidFlowPDEComponent. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FluidFlowPDEComponent.html 年