Wolfram言語＆システムドキュメントセンター

FunctionBijective[f,x]

が各 y∈Realsについて厳密に1つの解 x∈Realsを持つかどうかを調べる．

FunctionBijective[f,x,dom]

が各 y∈dom について厳密に1つの解 x∈dom を持つかどうかを調べる．

FunctionBijective[{f₁,f₂,…},{x₁,x₂,…},dom]

が各 y₁,y₂,…∈dom について厳密に1つの解 x₁,x₂,…∈dom を持つかどうかを調べる．

FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom]

が，ycons によって制限された各 yvars∈dom に対して制約 xcons によって制限された厳密に1つの解 xvars∈dom を持つかどうかを調べる．

FunctionBijective

FunctionBijective[f,x]

が各 y∈Realsについて厳密に1つの解 x∈Realsを持つかどうかを調べる．

FunctionBijective[f,x,dom]

が各 y∈dom について厳密に1つの解 x∈dom を持つかどうかを調べる．

FunctionBijective[{f₁,f₂,…},{x₁,x₂,…},dom]

が各 y₁,y₂,…∈dom について厳密に1つの解 x₁,x₂,…∈dom を持つかどうかを調べる．

FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom]

が，ycons によって制限された各 yvars∈dom に対して制約 xcons によって制限された厳密に1つの解 xvars∈dom を持つかどうかを調べる．

詳細とオプション

全単射関数は，一対一の関数あるいは上への関数としても知られている．
各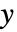について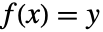となるような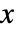が厳密に1つあるなら，関数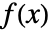は全単射である．

写像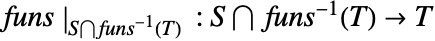が全単射ならば，FunctionBijective[{funs,xcons,ycons},xvars,yvars,dom]はTrueを返す．ただし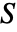，は xcons の解集合で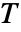は ycons の解集合である．
funs が xvars 以外のパラメータを含んでいる場合は，結果がConditionalExpressionであることが多い．
dom の可能な値はRealsとComplexesである．dom がRealsなら，変数，パラメータ，定数，関数値はすべて実数でなければならない．
funs の領域はFunctionDomainが与える条件で制限される．
xcons および ycons は，等式，不等式，それらの論理結合を含むことができる．
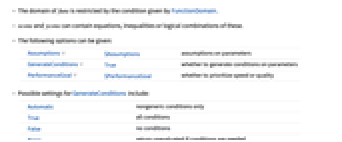
次は使用可能なオプションンである．

Assumptions	$Assumptions	パラメータについての仮定
GenerateConditions	True	パラメータについての条件を生成するかどうか
PerformanceGoal	$PerformanceGoal	速度と品質のどちらかを優先するかどうか

GenerateConditionsの可能な設定には以下がある．

	Automatic	一般的ではない条件のみ
	True	すべての条件
	False	条件なし
	None	条件が必要な場合には未評価で返す

PerformanceGoalの可能な設定には"Speed"と"Quality"がある．

例題

すべて開くすべて閉じる

例 (4)

一変量関数の実数上での全単射性を調べる：

Wolfram Language code: FunctionBijective[Sinh[x], x]

複素数上での全単射性を調べる：

Wolfram Language code: FunctionBijective[Sinh[x], x, Complexes]

実数上での多項式写像の全単射性を調べる：

Wolfram Language code: FunctionBijective[{x + y ^ 3, y - x ^ 5}, {x, y}]

記号係数を持つ多項式の全単射性を調べる：

Wolfram Language code: FunctionBijective[x ^ 3 + a x + b, x]

スコープ (10)

実数上の全単射性：

Wolfram Language code: FunctionBijective[x ^ 3 - x, x]

一部の値には複数回達する：

Wolfram Language code: Plot[{x ^ 3 - x, 1 / 4}, {x, -2, 2}]

実数の部分集合間の全単射性：

Wolfram Language code: FunctionBijective[{x ^ 3 - x, x > 1, y > 0}, x, y]

のときは，正の各値に厳密に1回達する：

Wolfram Language code: Plot[{x ^ 3 - x, 10}, {x, 1, 3}]

複素数上の全単射性：

Wolfram Language code: FunctionBijective[Log[x], x, Complexes]

達しない値もある：

Wolfram Language code: Reduce[Log[x] == y, x]

対数はのとき上へ全単射である：

Wolfram Language code: FunctionBijective[{Log[x], True, -Pi < Im[y] ≤ Pi}, x, y, Complexes]

複素数の部分集合上の全単射性：

Wolfram Language code: FunctionBijective[{x ^ 4, Re[x] ≥ 0 && Im[x] > 0 || x == 0}, x, Complexes]

は複素平面全体では全単射ではない：

Wolfram Language code: FunctionBijective[x ^ 4, x, Complexes]

複数回達せられる値もある：

Wolfram Language code: Reduce[x ^ 4 == 1, x]

整数上の全単射性：

Wolfram Language code: FunctionBijective[{x + 1, Element[x, Integers], Element[y, Integers]}, x, y]

線形写像の全単射性：

Wolfram Language code: A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};

Wolfram Language code: FunctionBijective[A.{x, y, z}, {x, y, z}]

Wolfram Language code: B = {{1, 2, 3}, {4, 5, 6}, {7, 8, 0}};

Wolfram Language code: FunctionBijective[B.{x, y, z}, {x, y, z}]

行列が正方行列で最大階数であるときかつそのときに限り線形写像は全単射である：

Wolfram Language code: {MatrixRank[A], MatrixRank[B]}

多項式写像の全単射性：

Wolfram Language code: FunctionBijective[{x ^ 3 - 3x y ^ 2, 3x ^ 2y - y ^ 3}, {x, y}]

の実部と虚部に等しい制限された写像 $TemplateBox[{}, NonNegativeReals]^2->TemplateBox[{}, Reals]^2\(TemplateBox[{}, PositiveReals]xTemplateBox[{}, NegativeReals])$ は全単射である：

Wolfram Language code: FunctionBijective[{{x ^ 3 - 3x y ^ 2, 3x ^ 2y - y ^ 3}, x ≥ 0 && y ≥ 0, u ≤ 0 || v ≥ 0}, {x, y}, {u, v}]

多項式写像の全単射性：

Wolfram Language code: FunctionBijective[{x + y ^ 3, y - x ^ 5}, {x, y}, Complexes]

全単射複素多項式写像のヤコビの行列式は一定でなければならない：

Wolfram Language code: Det[D[{x + y ^ 3, y - x ^ 5}, {{x, y}}]]

ヤコビアン予想には逆含意が真であるとある：

Wolfram Language code: Det[D[{x - (x + y / 27) ^ 3, y + (3 x + y / 9) ^ 3}, {{x, y}}]]

たしかに，一定のヤコビアンを持つこの多項式写像は全単射である：

Wolfram Language code: FunctionBijective[{x - (x + y / 27) ^ 3, y + (3 x + y / 9) ^ 3}, {x, y}, Complexes]

記号パラメータを持つ実多項式の全単射性：

Wolfram Language code: FunctionBijective[x ^ 3 + a x ^ 2 + b x + c, x]

記号パラメータを持つ実多項式写像の全単射性：

Wolfram Language code: FunctionBijective[{x + a y ^ 3, y + b x ^ 3}, {x, y}]

オプション (4)

Assumptions (1)

FunctionBijectiveはここでは条件付きの答を与える：

Wolfram Language code: FunctionBijective[{x + a y ^ 3, y + 2 x ^ 3}, {x, y}]

次はの残りの実数値についての全単射性をチェックする：

Wolfram Language code: FunctionBijective[{x + a y ^ 3, y + 2 x ^ 3}, {x, y}, Assumptions -> a > 0]

GenerateConditions (2)

デフォルトで，FunctionBijectiveは記号パラメータについての条件を生成することがある：

Wolfram Language code: FunctionBijective[x ^ 3 + a x ^ 2 + b x + c, x]

GenerateConditions->Noneのとき，FunctionBijectiveは条件付きの結果を与える代りに失敗する：

Wolfram Language code: FunctionBijective[x ^ 3 + a x ^ 2 + b x + c, x, GenerateConditions -> None]

以下は条件的に有効な結果を条件を述べずに返す：

Wolfram Language code: FunctionBijective[x ^ 3 + a x ^ 2 + b x + c, x, GenerateConditions -> False]

デフォルトで，すべての条件が報告される：

Wolfram Language code: FunctionBijective[a x, x, Complexes]

GenerateConditions->Automaticとすると，一般的に真である条件は報告されない：

Wolfram Language code: FunctionBijective[a x, x, Complexes, GenerateConditions -> Automatic]

PerformanceGoal (1)

PerformanceGoalを使って潜在的に高価な計算を避ける：

Wolfram Language code: FunctionBijective[x ^ 5 + a x ^ 4 + b x ^ 3 + c x ^ 2 + d x, x, PerformanceGoal -> "Speed"]

デフォルト設定は使用可能なすべてのテクニックを使って結果を出そうとする：

Wolfram Language code: FunctionBijective[x ^ 5 + a x ^ 4 + b x ^ 3 + c x ^ 2 + d x, x]

アプリケーション (11)

基本的なアプリケーション (8)

の全単射性をチェックする：

Wolfram Language code: FunctionBijective[x ^ 3, x]

各値には厳密に1回達する：

Wolfram Language code: Plot[{x ^ 3, -3, 3}, {x, -2, 2}]

は全単射ではない：

Wolfram Language code: FunctionBijective[x ^ 3 - x, x]

例えばのような値には複数回達する：

Wolfram Language code: Plot[{x ^ 3 - x, 1 / 4}, {x, -2, 2}]

は全単射ではない：

Wolfram Language code: FunctionBijective[ArcTan[x], x]

例えばのような値には達しない：

Wolfram Language code: Plot[{ArcTan[x], 2}, {x, -5, 5}]

はその実領域において全単射である：

Wolfram Language code: FunctionBijective[Log[x], x]

各値には厳密に1回達する：

Wolfram Language code: Plot[{Log[x], -1, 1}, {x, 0, 5}]

が全単射であることを示す：

Wolfram Language code: FunctionBijective[SinhIntegral[x], x]

Wolfram Language code: Plot[SinhIntegral[x], {x, -5, 5}]

は全単射ではないことを示す：

Wolfram Language code: FunctionBijective[Hyperfactorial[x], x]

Wolfram Language code: Plot[Hyperfactorial[x], {x, -1, 2}]

関数は，単射かつ全射のときかつそのときに限り全単射である：

Wolfram Language code: FunctionInjective[x ^ 3 / (x ^ 2 + 1), x]

Wolfram Language code: FunctionSurjective[x ^ 3 / (x ^ 2 + 1), x]

Wolfram Language code: FunctionBijective[x ^ 3 / (x ^ 2 + 1), x]

Wolfram Language code: Plot[x ^ 3 / (x ^ 2 + 1), {x, -1, 1}]

は単射ではないので全単射ではない：

Wolfram Language code: FunctionInjective[x Sin[x], x]

Wolfram Language code: FunctionBijective[x Sin[x], x]

Wolfram Language code: Plot[x Sin[x], {x, -20, 20}]

は全射ではないので全単射ではない：

Wolfram Language code: FunctionSurjective[Erf[x], x]

Wolfram Language code: FunctionBijective[Erf[x], x]

Wolfram Language code: Plot[Erf[x], {x, -5, 5}]

任意の水平線が関数のグラフと厳密に1回交差するなら，その関数は全単射である：

Wolfram Language code: f = (3x ^ 7 + 3x ^ 2 + x ^ 3) / (x ^ 6 + 2x ^ 2);

Wolfram Language code: FunctionBijective[f, x]

Wolfram Language code: Manipulate[Plot[{f, a}, ...], {{a, 1.5}, -5, 5}]

は全単射ではない：

Wolfram Language code: FunctionBijective[SinIntegral[x], x]

水平線の中にはグラフと複数回交差するものがあり，全く交差しないものもある：

Wolfram Language code: Manipulate[Plot[{SinIntegral[x], a}, ...], {{a, 1.5}, -3, 3}]

全単射関数の合成関数は全単射である：

Wolfram Language code: FunctionBijective[x ^ 3, x]

Wolfram Language code: FunctionBijective[Sinh[x], x]

Wolfram Language code: FunctionBijective[#, x]& /@ {Sinh[x ^ 3], Sinh[x] ^ 3}

が与えるアフィン写像 $TemplateBox[{}, Reals]^n->TemplateBox[{}, Reals]^n$ は，の階数がと等しいなら全単射である：

Wolfram Language code: Subscript[A, 1] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 0}};

Wolfram Language code: MatrixRank[Subscript[A, 1]]

Wolfram Language code: FunctionBijective[Subscript[A, 1].{x, y, z} + {1, 2, 3}, {x, y, z}]

Wolfram Language code: Subscript[A, 2] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};

Wolfram Language code: MatrixRank[Subscript[A, 2]]

Wolfram Language code: FunctionBijective[Subscript[A, 2].{x, y, z} + {1, 2, 3}, {x, y, z}]

確率 (1)

厳密に正のPDFの分布のCDFは上への全単射である：

Wolfram Language code: pdf = PDF[NormalDistribution[], x]

Wolfram Language code: FunctionSign[pdf, x]

Wolfram Language code: Plot[pdf, {x, -5, 5}]

Wolfram Language code: cdf = CDF[NormalDistribution[], x]

Wolfram Language code: FunctionBijective[{cdf, True, 0 < y < 1}, x, y]

Wolfram Language code: Plot[cdf, {x, -3, 3}]

SurvivalFunctionも上への全単射である：

Wolfram Language code: sf = SurvivalFunction[NormalDistribution[], x]

Wolfram Language code: FunctionBijective[{sf, True, 0 < y < 1}, x, y]

Wolfram Language code: Plot[sf, {x, -5, 5}]

Quantileは実数上への全単射である：

Wolfram Language code: qf = Quantile[NormalDistribution[], x]

Wolfram Language code: FunctionBijective[qf, x]

Wolfram Language code: Plot[qf, {x, 0, 1}]

微積分 (2)

変数を変えることでを計算する：

Wolfram Language code: e = Exp[-(x ^ 3 + y ^ 2) ^ 2] / (y ^ 6 + 1)x ^ 2y ^ 2;

が全単射写像であるなら $int_Uf(g(u)) TemplateBox[{TemplateBox[{{{(, {partial, g}, )}, /, {(, {partial, u}, )}}}, Det]}, Abs]du=int_Vf(v)dv$ である：

Wolfram Language code: f[{u_, v_}] := 1 / 9Exp[-u ^ 2] / (v ^ 2 + 1)

Wolfram Language code: g = {x ^ 3 + y ^ 2, y ^ 3};

Wolfram Language code: f[g]Det[D[g, {{x, y}}]] === e

が全単射写像 $TemplateBox[{}, Reals]^2->TemplateBox[{}, Reals]^2$ であることを確かめる：

Wolfram Language code: FunctionBijective[g, {x, y}]

積分を計算する：

Wolfram Language code: Integrate[f[{u, v}], {u, -Infinity, Infinity}, {v, -Infinity, Infinity}]

もとの積分を直接計算する：

Wolfram Language code: Integrate[e, {x, -Infinity, Infinity}, {y, -Infinity, Infinity}]

半径の球の表面積を有理パラメータ化を使って計算する：

Wolfram Language code: f = {(2 r (1 - t^2) u/(1 + t^2) (1 + u^2)), (4 r t u/(1 + t^2) (1 + u^2)), (r (1 - u^2)/1 + u^2)};

Wolfram Language code: ParametricPlot3D[Evaluate[f /. r -> 1], {t, -50, 50}, {u, 0, 50}, ...]

パラメータ化が低次元集合を除いて球上への全単射であることを確かめる：

Wolfram Language code:

FunctionBijective[{f, u > 0, x ^ 2 + y ^ 2 + z ^ 2 == r ^ 2 && (y ≠ 0 || x > 0)}, {t, u}, {x, y, z}, Assumptions -> r > 0]

表面積はのグラム行列式の平方根の積分に等しい：

Wolfram Language code: df = D[f, {{t, u}}];

Wolfram Language code: Integrate[Sqrt[Det[Transpose[df].df]], {u, 0, ∞}, {t, -∞, ∞}, Assumptions -> r > 0]

特性と関係 (3)

方程式が各について厳密に1つの解を持つときかつそのときに限り，は全単射である：

Wolfram Language code: FunctionBijective[x ^ 2 + x + 1, x]

Wolfram Language code: FunctionBijective[x ^ 3 + x + 1, x]

Solveを使って解を求める：

Wolfram Language code: Solve[x ^ 2 + x + 1 == y, x, Reals]

Wolfram Language code: Solve[x ^ 3 + x + 1 == y, x, Reals]

ある区間についての連続実数関数は，単調で端点の極限がとであるときかつそのときに限り全単射である：

Wolfram Language code: FunctionBijective[{Sec[x], -Pi / 2 < x < Pi / 2}, x]

Wolfram Language code: FunctionBijective[{Tan[x], -Pi / 2 < x < Pi / 2}, x]

Wolfram Language code: Plot[{Sec[x], Tan[x]}, {x, -Pi / 2, Pi / 2}]

FunctionMonotonicityを使って関数の単調性を判断する：

Wolfram Language code: FunctionMonotonicity[{Sec[x], -Pi / 2 < x < Pi / 2}, x]

Wolfram Language code: FunctionMonotonicity[{Tan[x], -Pi / 2 < x < Pi / 2}, x]

Limitを使って極限を計算する：

Wolfram Language code: Limit[{Sec[x], Tan[x]}, x -> -Pi / 2, Direction -> "FromAbove"]

Wolfram Language code: Limit[{Sec[x], Tan[x]}, x -> Pi / 2, Direction -> "FromBelow"]

複素多項式写像は，それが逆多項式を持つときかつそのときに限り多項式全単射である：

Wolfram Language code: F = {x - (x + y / 27) ^ 3, y + (3 x + y / 9) ^ 3};

Wolfram Language code: FunctionBijective[F, {x, y}, Complexes]

Solveを使って逆多項式を求める：

Wolfram Language code: G = {x, y} /. Solve[{u, v} == {x - (x + y / 27) ^ 3, y + (3 x + y / 9) ^ 3}, {x, y}][[1]]

はの両側逆元であることを確かめる：

Wolfram Language code: Expand[G /. Thread[{u, v} -> F]]

Wolfram Language code: Expand[F /. Thread[{x, y} -> G]]

考えられる問題 (2)

FunctionBijectiveはFunctionDomainを使って関数の実領域を決定する：

Wolfram Language code: FunctionBijective[{Cosh[Sqrt[x]], True, y ≥ 1}, x, y]//Quiet

はFunctionDomainによって報告された実領域で上へ全単射である：

Wolfram Language code: FunctionDomain[Cosh[Sqrt[x]], x]

Wolfram Language code: Plot[{Cosh[Sqrt[x]], 7}, {x, 0, 10}]

は全実領域では，実数値で上へ全単射ではない：

Wolfram Language code: Plot[{Cosh[Sqrt[x]], -1 / 2}, {x, -20, 10}]

ある点がの実領域に属するためには．の部分式のすべてが実数値でなければならない：

Wolfram Language code: Refine[Element[Sqrt[x], Reals], x < 0]

FunctionBijectiveは領域を ycons の解集合の逆像に制限する：

Wolfram Language code: FunctionBijective[{x / 2, Element[x, Integers], Element[y, Integers]}, x, y]

2による除算は，偶数の整数（整数の逆像）と整数の間の全単射である．

Top

その他のラーニングリソース

テクニカルサポート

データサイエンス，金融，ビジネス

工学

科学とテクノロジー

教育のためのテクノロジー

教育イニシアチブ

使い始める

Grow Your Skills

Wolframと繋がる

大人用の教育プログラム

若者のための教育プログラム

読む

FunctionBijective

詳細とオプション

例題

例 (4)

スコープ (10)

オプション (4)

Assumptions (1)

GenerateConditions (2)

PerformanceGoal (1)

アプリケーション (11)

基本的なアプリケーション (8)

確率 (1)

微積分 (2)

特性と関係 (3)

考えられる問題 (2)

テキスト

CMS

APA

BibTeX

BibLaTeX

FunctionBijective

詳細とオプション

例題

例 (4)

スコープ (10)

オプション (4)

Assumptions (1)

GenerateConditions (2)

PerformanceGoal (1)

アプリケーション (11)

基本的なアプリケーション (8)

確率 (1)

微積分 (2)

特性と関係 (3)

考えられる問題 (2)

関連項目

関連するガイド

履歴

テキスト

CMS

APA

BibTeX

BibLaTeX