WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

FunctionSurjective
✖
FunctionSurjective

✖

tests whether has at least one solution x in TemplateBox[{}, Reals] for each y∈Reals.

✖

tests whether has at least one solution x∈dom for each y∈dom.

✖
FunctionSurjective[{f1,f2,…},{x1,x2,…},dom]

tests whether has at least one solution x1,x2,…∈dom for each y1,y2,…∈dom.

✖
FunctionSurjective[{funs,xcons,ycons},xvars,yvars,dom]

tests whether has at least one solution with xvars∈dom restricted by the constraints xcons for each yvars∈dom restricted by the constraints ycons.

Details and Options

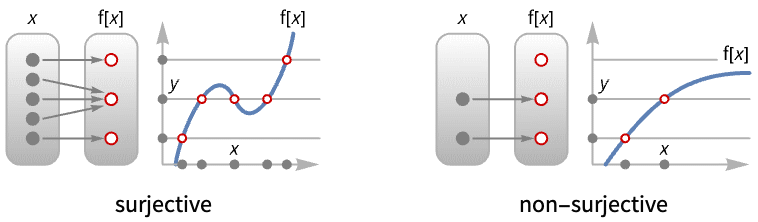
  • A surjective function is also known as onto or an onto mapping.
  • A function 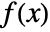is surjective if for every 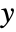there is at least one 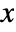such that .
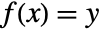  • If funs contains parameters other than xvars, the result is typically a ConditionalExpression.
  • Possible values for dom are Reals and Complexes. If dom is Reals, then all variables, parameters, constants and function values are restricted to be real.
  • The domain of funs is restricted by the condition given by FunctionDomain.
  • xcons and ycons can contain equations, inequalities or logical combinations of these.
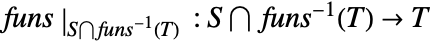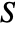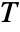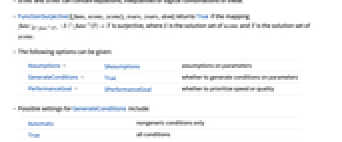
  • FunctionSurjective[{funs,xcons,ycons},xvars,yvars,dom] returns True if the mapping is surjective, where is the solution set of xcons and is the solution set of ycons.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters
    GenerateConditions Truewhether to generate conditions on parameters
    PerformanceGoal $PerformanceGoalwhether to prioritize speed or quality
  • Possible settings for GenerateConditions include:
  • Automaticnongeneric conditions only
    Trueall conditions
    Falseno conditions
    Nonereturn unevaluated if conditions are needed
  • Possible settings for PerformanceGoal are "Speed" and "Quality".

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Test surjectivity of a univariate function over the reals:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-b2fcqx
Out[1]=1

Test surjectivity over the complexes:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-0dl46
Out[1]=1

Test surjectivity of a polynomial mapping over the reals:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-dp3h13
Out[1]=1

Test surjectivity of a polynomial with symbolic coefficients:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-kqrk3c
Out[1]=1

Scope  (12)Survey of the scope of standard use cases

Surjectivity over the reals:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-gxhl11
Out[1]=1

Each value is attained at least once:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-d5ri0g
Out[2]=2

Surjectivity over a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-glvby
Out[1]=1

For positive , some values are not attained:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-h18c7
Out[2]=2

Surjectivity onto a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-d66d8y
Out[1]=1

Each positive value is for some positive :

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-ctca0g
Out[2]=2

Surjectivity over the complexes:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-gb8vpl
Out[1]=1

The value zero is not attained:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-unv0t
Out[2]=2

Surjectivity onto a subset of complexes:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-e5opda
Out[1]=1

Surjectivity over the integers:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-oypp7s
Out[1]=1

Surjectivity of linear mappings:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-fuu3lu
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-dw1lhm
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-bb3g0a
In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-huze44
Out[4]=4

A linear mapping is surjective iff the rank of its matrix is equal to the dimension of its codomain:

In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-dwvhdm
Out[5]=5

Surjectivity of polynomial mappings :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-en7wnr
Out[1]=1

Each value is attained at least once:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-bccrwp
Out[2]=2

This mapping is not surjective:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-hdmdbu
Out[3]=3

Some values are not attained:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-hh23j9
Out[4]=4

Surjectivity of polynomial mappings :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-dcji69
Out[1]=1

Surjectivity of polynomial mappings :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-dcz40b
Out[1]=1

Surjectivity of a real polynomial with symbolic parameters:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-dqtdtb
Out[1]=1

Surjectivity of a real polynomial mapping with symbolic parameters:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-yju7
Out[1]=1

Options  (4)Common values & functionality for each option

Assumptions  (1)

FunctionSurjective gives a conditional answer here:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-bnv0jw
Out[1]=1

This checks the surjectivity for the remaining real values of :

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-c50qtk
Out[2]=2

GenerateConditions  (2)

By default, FunctionSurjective may generate conditions on symbolic parameters:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-osy2z
Out[1]=1

With GenerateConditionsNone, FunctionSurjective fails instead of giving a conditional result:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-fe9ubz
Out[2]=2

This returns a conditionally valid result without stating the condition:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-na5ydu
Out[3]=3

By default, all conditions are reported:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-tdcquw
Out[1]=1

With GenerateConditionsAutomatic, conditions that are generically true are not reported:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-291b1m
Out[2]=2

PerformanceGoal  (1)

Use PerformanceGoal to avoid potentially expensive computations:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-i86kxj
Out[1]=1

The default setting uses all available techniques to try to produce a result:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-i9gq
Out[2]=2

Applications  (11)Sample problems that can be solved with this function

Basic Applications  (7)

Check surjectivity of :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-tmkzs
Out[1]=1

is surjective because it attains each value at least once:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-hwemwk
Out[2]=2

Check surjectivity of :

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-5p94k
Out[3]=3

is not surjective because the value is not attained:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-dob2rz
Out[4]=4

is not surjective because it does not attain negative values:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-rz87j
Out[1]=1

The value is not attained:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-fhmver
Out[2]=2

is surjective as a function from TemplateBox[{}, NonNegativeReals] to TemplateBox[{}, NonNegativeReals]:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-kz0n6
Out[3]=3

Each non-negative value is attained:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-g0ztcj
Out[4]=4

is surjective:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-g639dg
Out[1]=1

Each value is attained at least once:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-smrt9
Out[2]=2

TemplateBox[{x}, CosIntegral] is not surjective:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-b1wh39
Out[3]=3

Some values, e.g. , are not attained:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-eidcke
Out[4]=4

A function is surjective if any horizontal line intersects its graph at least once:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-bethas
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-djdklc
Out[2]=2

If a horizontal line does not intersect the graph, the function is not surjective:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-hybo03
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-p3tdpb
Out[4]=4

is bounded:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-mi5ep
Out[1]=1

Bounded functions are not surjective:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-hfe8tb
Out[2]=2

If is continuous on and , then is surjective onto :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-k79eri
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-i5xwge
Out[2]=2

Use FunctionContinuous to check that is continuous in :

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-gwhxce
Out[3]=3

By the intermediate value theorem, restricted to is surjective onto :

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-chr9a
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-bx6mvx
Out[5]=5

An affine mapping is surjective if the rank of is equal to the number of rows of :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-m9q295
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-hq1fwk
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-bet2ie
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-fclhyh
In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-d64ko
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/08umqdsvoau4aui-cp7s2y
Out[6]=6

Solving Equations and Inequalities  (1)

A function is surjective if the equation has at least one solution for any :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-c2h13o
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-fsca99
Out[2]=2

For each real , there is at least one real solution for :

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-fnkkdu
Out[3]=3

Use Resolve to check the condition expressed using quantifiers:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-dvrfk3
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-k28m21
Out[5]=5

Probability & Statistics  (3)

A CDF for a continuous distribution is surjective onto the interval of probabilities (0,1) over its domain:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-l16efo
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-bybrxp
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-e654vt
Out[3]=3

A SurvivalFunction for a continuous distribution is surjective onto the interval of probabilities (0,1) over its domain:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-fvov3m
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-oxfmxd
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-bgw7z
Out[3]=3

The quantile function Quantile for a distribution is surjective onto the domain of the distribution:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-bas5y6
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-bp1vf1
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-c3w06j
Out[3]=3

Properties & Relations  (3)Properties of the function, and connections to other functions

is surjective iff the equation has at least one solution for each :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-bgha30
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-fgftkt
Out[2]=2

Use Solve to find the solutions:

In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-h9imdc
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-ec0f5e
Out[4]=4

A real continuous function on an interval is surjective iff the limits at endpoints are and :

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-b0d3so
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-mtrqj2
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-daqrl2
Out[3]=3

Use Limit to compute the limits:

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-fmt43q
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-if28q4
Out[5]=5

A function is surjective if its FunctionRange is True:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-jwh4ee
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-e842wa
Out[2]=2

Possible Issues  (1)Common pitfalls and unexpected behavior

FunctionSurjective determines the real domain of functions using FunctionDomain:

In[1]:=1
✖
https://wolfram.com/xid/08umqdsvoau4aui-c1rnh7
Out[1]=1

is not surjective onto in the real domain reported by FunctionDomain:

In[2]:=2
✖
https://wolfram.com/xid/08umqdsvoau4aui-gfcxum
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/08umqdsvoau4aui-e806up
Out[3]=3

is real valued over the whole reals and is surjective onto :

In[4]:=4
✖
https://wolfram.com/xid/08umqdsvoau4aui-bhmdzf
Out[4]=4

All subexpressions of need to be real valued for a point to belong to the real domain of :

In[5]:=5
✖
https://wolfram.com/xid/08umqdsvoau4aui-h3a0uv
Out[5]=5
Wolfram Research (2020), FunctionSurjective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSurjective.html.
✖
Wolfram Research (2020), FunctionSurjective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSurjective.html.

Text

Wolfram Research (2020), FunctionSurjective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSurjective.html.

✖
Wolfram Research (2020), FunctionSurjective, Wolfram Language function, https://reference.wolfram.com/language/ref/FunctionSurjective.html.

CMS

Wolfram Language. 2020. "FunctionSurjective." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSurjective.html.

✖
Wolfram Language. 2020. "FunctionSurjective." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSurjective.html.

APA

Wolfram Language. (2020). FunctionSurjective. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSurjective.html

✖
Wolfram Language. (2020). FunctionSurjective. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSurjective.html

BibTeX

@misc{reference.wolfram_2025_functionsurjective, author="Wolfram Research", title="{FunctionSurjective}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSurjective.html}", note=[Accessed: 21-April-2025 ]}

✖
@misc{reference.wolfram_2025_functionsurjective, author="Wolfram Research", title="{FunctionSurjective}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/FunctionSurjective.html}", note=[Accessed: 21-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_functionsurjective, organization={Wolfram Research}, title={FunctionSurjective}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSurjective.html}, note=[Accessed: 21-April-2025 ]}

✖
@online{reference.wolfram_2025_functionsurjective, organization={Wolfram Research}, title={FunctionSurjective}, year={2020}, url={https://reference.wolfram.com/language/ref/FunctionSurjective.html}, note=[Accessed: 21-April-2025 ]}