GaborMatrix

GaborMatrix[r,k]

半径 r で波動ベクトルが k のGaborカーネルの実部に対応する行列を与える．

GaborMatrix[r,k,ϕ]

位相変位 ϕ を使う．

GaborMatrix[{r,σ},…]

指定された標準偏差 σ を使う．

GaborMatrix[{{r1,r2,…}},…]

第 i 指標方向で半径が ri のGaborカーネルに対応する配列を与える．

詳細とオプション

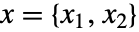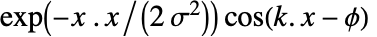  • GaborMatrix[{r,σ},k,ϕ]は中心からの指標位置 でに比例する値を与える．
  • GaborMatrix[r,k]はGaborMatrix[{r,r/2},k,0]と等価である．
  • デフォルトで，行列はAbs[GaborMatrix[r,k,0]+I GaborMatrix[r,k,π/2]]の要素の和が1になるように再スケールされる．
  • 整数 r については，GaborMatrix[r,…]は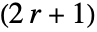×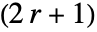行列を返す．
  • 非整数 r については，r の値は事実上整数に丸められる．
  • r あるいは σ のどちらかは，異なる方向に対して異なる値を指定するリストでよい．
  • GaborMatrix[{r,{σ1,σ2,…}},k]のとき，σ1 は k と並ぶ標準偏差であり，σ2, …は k と垂直の標準偏差である．i 番目の方向はRotationMatrix[{{1,0,…},k}]の第 i 列によって定義される．
  • n 個の次元と波動ベクトル{k1,…,kn}を持つ data 配列では，kiは data の i 次元と同じ方向を向いている．画像の場合は，このフィルタは事実上ImageData[image]に適用される．
  • 指定可能なオプション
  • Standardized True切断を説明するために行列を再スケールするかどうか
    WorkingPrecision Automatic行列要素を計算する精度

例題

すべて開くすべて閉じる

例  (3)

Gabor行列を可視化する：

Gabor行列のMatrixPlot：

1DのGaborベクトル：

スコープ  (9)

45°の波動ベクトルを使ったGabor行列．波動ベクトルが波面と垂直である点に注意：

等方性の標準偏差 を指定する：

異方性の標準偏差 および を指定する：

波長の長いGabor行列を得るために波の数を減らす：

矩形Gabor行列を作る：

波長が長くノードが中央にある異方性Gabor行列：

さまざまな波数と位相変位で1DのGaborベクトルを可視化する：

1DのGaborベクトルの振幅スペクトルを，波数を変えて可視化する：

3DのGabor行列：

オプション  (2)

Standardized  (1)

デフォルト設定はTrueである：

StandardizedFalseを使う：

WorkingPrecision  (1)

デフォルトでMachinePrecisionが使われる：

代りに厳密計算を行う：

特性と関係  (3)

GaborFilterはGaborMatrixによるたたみ込みと等しい：

自身と等価であるGaborウェーブレット関数上の1DのGaborカーネルを可視化する：

波長0の波動ベクトルのとき，Gabor行列はGaussianMatrixと等価である：

Wolfram Research (2012), GaborMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaborMatrix.html （2015年に更新）.

テキスト

Wolfram Research (2012), GaborMatrix, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaborMatrix.html （2015年に更新）.

CMS

Wolfram Language. 2012. "GaborMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GaborMatrix.html.

APA

Wolfram Language. (2012). GaborMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaborMatrix.html

BibTeX

@misc{reference.wolfram_2024_gabormatrix, author="Wolfram Research", title="{GaborMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaborMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gabormatrix, organization={Wolfram Research}, title={GaborMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaborMatrix.html}, note=[Accessed: 22-November-2024 ]}