GaborMatrix

GaborMatrix[r,k]

gives a matrix that corresponds to the real part of a Gabor kernel of radius r and wave vector k.

GaborMatrix[r,k,ϕ]

uses phase shift ϕ.

GaborMatrix[{r,σ},…]

uses the specified standard deviation σ.

GaborMatrix[{{r1,r2,…}},…]

gives an array corresponding to a Gabor kernel with radius ri in the i^(th) index direction.

Details and Options

  • GaborMatrix[{r,σ},k,ϕ] gives values proportional to 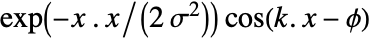at index position 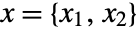from the center.
  • GaborMatrix[r,k] is equivalent to GaborMatrix[{r,r/2},k,0].
  • By default, the matrix is rescaled so that the elements of Abs[GaborMatrix[r,k,0]+I GaborMatrix[r,k,π/2]] sum to 1.
  • For integer r, GaborMatrix[r,…] yields a 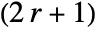× 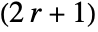matrix.
  • For noninteger r, the value of r is effectively rounded to an integer.
  • Either of the r or σ can be lists, specifying different values for different directions.
  • With GaborMatrix[{r,{σ1,σ2,…}},k], σ1 is the standard deviation along k, and σ2, … are standard deviations perpendicular to k. The i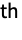^(th) direction is defined by the i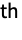^(th) column of RotationMatrix[{{1,0,…},k}].
  • For data arrays with n dimensions and a wave vector {k1,…,kn}, ki is pointing in the same direction as the i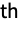^(th) dimension of data. For images, the filter is effectively applied to ImageData[image].
  • The following options can be specified:
  • Standardized Truewhether to rescale the matrix to account for truncation
    WorkingPrecision Automaticthe precision with which to compute matrix elements

Examples

open allclose all

Basic Examples  (3)

Visualize a Gabor matrix:

MatrixPlot of a Gabor matrix:

1D Gabor vector:

Scope  (9)

Gabor matrix using a 45° wave vector. Notice that the wave vector is perpendicular to the wave front:

Specify an isotropic standard deviation :

Specify an anisotropic standard deviation and :

Decrease the wave number to get a Gabor matrix with a larger wavelength:

Create a rectangular Gabor matrix:

An anisotropic Gabor matrix with a large wavelength and a node at the center:

Visualize a 1D Gabor vector with different wave number and phase shift:

Visualize the magnitude spectrum of a 1D Gabor vector for different values of the wavenumber:

A 3D Gabor matrix:

Options  (2)

Standardized  (1)

The default setting is True:

Use StandardizedFalse:

WorkingPrecision  (1)

MachinePrecision is used by default:

Perform exact computation instead:

Properties & Relations  (3)

GaborFilter is equivalent to a convolution with a GaborMatrix:

Visualize the 1D Gabor kernel on its equivalent Gabor wavelet function:

With a zero-length wave vector, Gabor matrix is equivalent to GaussianMatrix:

Wolfram Research (2012), GaborMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborMatrix.html (updated 2015).

Text

Wolfram Research (2012), GaborMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/GaborMatrix.html (updated 2015).

CMS

Wolfram Language. 2012. "GaborMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GaborMatrix.html.

APA

Wolfram Language. (2012). GaborMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaborMatrix.html

BibTeX

@misc{reference.wolfram_2024_gabormatrix, author="Wolfram Research", title="{GaborMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaborMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gabormatrix, organization={Wolfram Research}, title={GaborMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaborMatrix.html}, note=[Accessed: 22-November-2024 ]}