GaborMatrix

GaborMatrix[r,k]

给出对应于半径为 r，波长向量为 k 的 Gabor 核的实部的矩阵.

GaborMatrix[r,k,ϕ]

使用相位平移 ϕ.

GaborMatrix[{r,σ},…]

使用指定的标准差 σ.

GaborMatrix[{{r1,r2,…}},…]

给出对应于在第 i 索引方向上半径为 ri 的 Gabor 核的数组.

更多信息和选项

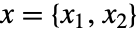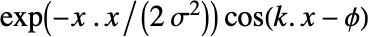  • GaborMatrix[{r,σ},k,ϕ] 给出从中心索引位置为 处与 成正比的值.
  • GaborMatrix[r,k] 等价于 GaborMatrix[{r,r/2},k,0].
  • 默认情况下，对矩阵进行尺度缩放，因此 Abs[GaborMatrix[r,k,0]+I GaborMatrix[r,k,π/2]] 的元素之和为 1.
  • 对于整数 r，GaborMatrix[r,…] 产生一个 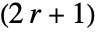× 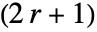矩阵.
  • 对于非整数 r，r 的值进行四舍五入得到一个整数.
  • r 或者 σ 可以为列表，指定不同方向的不同值.
  • 设置 GaborMatrix[{r,{σ1,σ2,…}},k]，σ1 是在 k 上的标准差，而 σ2, … 是与 k 垂直的标准差. 第 i 方向是由 RotationMatrix[{{1,0,…},k}] 的第 i 列定义的.
  • 对于维度为 n 和波长向量为 {k1,…,kn} 的 data 数组，ki 指向与 data 的第 i 维相同的方向. 对于图像，滤波器事实上应用于 ImageData[image].
  • 可以指定下列选项：
  • Standardized True是否对矩阵进行尺度缩放，以考虑截断
    WorkingPrecision Automatic用于计算矩阵元素的精度

范例

打开所有单元关闭所有单元

基本范例  (3)

可视化 Gabor 矩阵：

Gabor 矩阵的 MatrixPlot：

一维 Gabor 向量：

范围  (9)

使用 45° 波长向量的 Gabor 矩阵. 注意波长向量与波长前端垂直：

指定等方性的标准差 :

指定一个各向异性的标准差 和 ：

把波数减少，以获取具有较大波长的 Gabor 矩阵：

创建一个方形 Gabor 矩阵：

具有大波长和中心节点的各向异性的 Gabor 矩阵：

使用不同的波数和相位平移可视化一个一维 Gabor 向量：

可视化波数不同的一维 Gabor 向量的幅值谱：

三维 Gabor 矩阵：

选项  (2)

Standardized  (1)

默认设置为 True：

使用 StandardizedFalse：

WorkingPrecision  (1)

默认情况下，使用 MachinePrecision：

执行精确计算：

属性和关系  (3)

GaborFilter 等价于使用 GaborMatrix 的卷积：

在等价 Gabor 波函数上可视化一维 Gabor 核：

使用长度为零的波向量，Gabor 矩阵等价于 GaussianMatrix:

Wolfram Research (2012)，GaborMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GaborMatrix.html （更新于 2015 年）.

文本

Wolfram Research (2012)，GaborMatrix，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GaborMatrix.html （更新于 2015 年）.

CMS

Wolfram 语言. 2012. "GaborMatrix." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GaborMatrix.html.

APA

Wolfram 语言. (2012). GaborMatrix. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GaborMatrix.html 年

BibTeX

@misc{reference.wolfram_2024_gabormatrix, author="Wolfram Research", title="{GaborMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GaborMatrix.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gabormatrix, organization={Wolfram Research}, title={GaborMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/GaborMatrix.html}, note=[Accessed: 22-November-2024 ]}