GegenbauerC

GegenbauerC[n,m,x]

ゲーゲンバウア(Gegenbauer)多項式 TemplateBox[{n, m, x}, GegenbauerC]を与える．

GegenbauerC[n,x]

くりこみ形式TemplateBox[{{TemplateBox[{n, m, x}, GegenbauerC], /, m}, m, 0}, Limit2Arg] を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 整数 n や m について明示的な多項式が与えられる．
  • TemplateBox[{n, m, x}, GegenbauerC]は微分方程式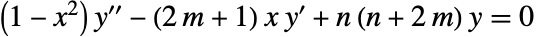を満たす．
  • ゲーゲンバウアの多項式は，単位超球においての積分に対応する，重みの関数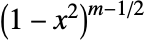とともに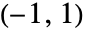，の区間において直交である．
  • 特別な引数の場合，GegenbauerCは，自動的に厳密値を計算する．
  • GegenbauerCは任意の数値精度で評価できる．
  • GegenbauerCは自動的にリストに縫い込まれる．
  • GegenbauerC[n,0,x]は常に0である．
  • GegenbauerC[n,m,z]は，複素 z 平面上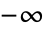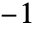，〜 の範囲で不連続な分枝切断線を持つ．
  • GegenbauerCはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

例題

すべて開くすべて閉じる

例  (7)

数値的に評価する：

十次のゲーゲンバウア多項式を計算する：

十次の再正規化されたゲーゲンバウア多項式を計算する：

実数の部分集合上でをプロットする：

複素数の部分集合上でプロットする：

原点における級数展開：

Infinityにおける漸近展開：

特異点における漸近展開：

スコープ  (44)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

高精度で効率よく評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のGegenbauerC関数を計算することもできる：

特定の値  (8)

固定点におけるGegenbauerCの値：

単純な場合は厳密な記号結果が与えられる：

記号的な n のGegenbauerC：

ゼロにおける値：

GegenbauerC[10,x ]の最初の正の最大値を求める：

陪多項式GegenbauerC[7,x]を計算する：

半整数 n について陪多項式GegenbauerC[1/2,x]を計算する：

異なるタイプのGegenbauerCは異なる記号形式を与える：

可視化  (4)

GegenbauerC関数をさまざまな次数でプロットする：

の実部をプロットする：

の虚部をプロットする：

2つのパラメータの実部が変化する様子をプロットする：

第2種と第3種のGegenbauerC関数の分岐構造は異なる：

関数の特性  (14)

整数次数の GegenbauerCの定義域：

整数次数のGegenbauerCの値域：

複素値の範囲は平面全体である：

奇次数のゲーゲンバウア多項式は奇多項式である：

偶次数のゲーゲンバウア多項式は偶数多項式である：

GegenbauerCは要素単位でリストに縫い込まれる：

GegenbauerCは鏡特性 を持つ：

ゲーゲンバウア多項式は解析的である：

しかし，GegenbauerC関数は，一般に，非整数パラメータについては解析的ではない：

有理型でもない：

TemplateBox[{2, x}, GegenbauerC2]は非減少でも非増加でもない：

TemplateBox[{2, x}, GegenbauerC2]は単射ではない：

TemplateBox[{2, x}, GegenbauerC2]は全射ではない：

TemplateBox[{2, x}, GegenbauerC2]は非負でも非正でもない：

TemplateBox[{n, x}, GegenbauerC2]は， が整数ではなく のとき特異点または不連続点を持つ：

TemplateBox[{n, m, x}, GegenbauerC]は， が非整数のときも特異点を持つ：

TemplateBox[{2, x}, GegenbauerC2]は凸である：

TraditionalFormによる表示：

微分  (3)

x についての一次導関数：

x についての高次導関数：

n=10かつ m=1/3のとき，x について高次導関数をプロットする：

x についての 次導関数の式：

積分  (3)

Integrateを使って不定積分を計算する：

不定積分を確かめる：

定積分：

その他の積分例：

級数展開  (2)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似のプロット：

生成点におけるテイラー展開：

関数の恒等式と簡約  (4)

GegenbauerCはJacobiPの特殊ケースである：

GegenbauerCの恒等式を微分する：

ゲーゲンバウア多項式の母関数：

漸化式：

一般化と拡張  (2)

GegenbauerCをベキ級数に適用する：

GegenbauerCは実数値区間を扱うことができる：

アプリケーション  (3)

四次元ラプラス演算子の角部分の固有関数：

運動量表示における水素原子固有関数のラジアル部分：

n 点のGauss–Lobatto求積法では，極端な2つのノードの値が固定され，他の n-2個のノードは特定のゲーゲンバウア多項式の根から計算される．n 点Gauss–Lobatto求積法のノードと重みを比較する：

n 点Gauss–Lobatto求積法を使って積分を数値的に評価する：

Gauss–Lobatto求積法の結果をNIntegrateの結果と比較する：

特性と関係  (5)

FunctionExpandを使ってGegenbauerCを他の関数に展開する：

GegenbauerCはDifferenceRootとして表すことができる：

GegenbauerCの級数展開における一般項：

GegenbauerCの母関数：

Integrateを使って関数の内積を定義する：

Orthogonalizeを使って正規直交基底を構築する：

この内積はGegenbauerC多項式を生成する：

考えられる問題  (1)

多項式の形における約分によって数値結果が不正確になることがある：

関数を直接評価する：

Wolfram Research (1988), GegenbauerC, Wolfram言語関数， https://reference.wolfram.com/language/ref/GegenbauerC.html （2022年に更新）.

テキスト

Wolfram Research (1988), GegenbauerC, Wolfram言語関数， https://reference.wolfram.com/language/ref/GegenbauerC.html （2022年に更新）.

CMS

Wolfram Language. 1988. "GegenbauerC." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/GegenbauerC.html.

APA

Wolfram Language. (1988). GegenbauerC. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GegenbauerC.html

BibTeX

@misc{reference.wolfram_2024_gegenbauerc, author="Wolfram Research", title="{GegenbauerC}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/GegenbauerC.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gegenbauerc, organization={Wolfram Research}, title={GegenbauerC}, year={2022}, url={https://reference.wolfram.com/language/ref/GegenbauerC.html}, note=[Accessed: 22-November-2024 ]}