GegenbauerC

GegenbauerC[n,m,x]

用来给出 Gegenbauer 多项式 TemplateBox[{n, m, x}, GegenbauerC].

GegenbauerC[n,x]

用来给出重正规化形式 TemplateBox[{{TemplateBox[{n, m, x}, GegenbauerC], /, m}, m, 0}, Limit2Arg].

更多信息

  • 数学函数， 同时适合符号和数值运算.
  • 对于整数 n 和任意 m 给出显式表达的多项式.
  • TemplateBox[{n, m, x}, GegenbauerC] 满足微分方程 .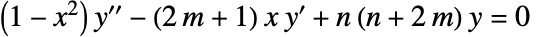
  • 加上权函数 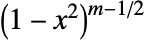，Gegenbauer 多项式在区间 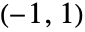上正交.
  • 对某些特定变量值，GegenbauerC 自动运算出精确值.
  • GegenbauerC 可计算到任意数值精度.
  • GegenbauerC 自动逐项作用于列表.
  • GegenbauerC[n,0,x] 总为零.
  • GegenbauerC[n,m,z] 在复平面 z 上从 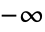到 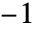的有一个不连续分支切割.
  • GegenbauerC 可与 Interval 和 CenteredInterval 对象一起使用. »

范例

打开所有单元关闭所有单元

基本范例  (7)

数值化计算：

计算 10 阶 Gegenbauer 多项式：

计算 10 阶重正规化的 Gegenbauer 多项式：

在实数的子集上绘制 ：

在复数的子集上绘图：

在原点的级数展开：

在 Infinity 的级数展开：

在奇点处的渐近展开式：

范围  (44)

数值计算  (6)

数值化计算：

高精度计算：

输出的精度与输入的精度一致：

复数输入：

高精度的高效计算：

用 Interval 和 CenteredInterval 对象计算最坏情况下的区间：

或用 Around 计算一般情况下的统计区间：

计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的 GegenbauerC 函数：

特殊值  (8)

在固定点的 GegenbauerC 的值：

简单情况给出精确符号结果：

符号 n 的 GegenbauerC:

零处的值：

求 GegenbauerC[10,x ] 的第一个正极大值：

计算相关的 GegenbauerC[7,x] 多项式：

计算半整数 n 的关联 GegenbauerC[1/2,x] 多项式:

不同的 GegenbauerC 类型给出不同的符号形式：

可视化  (4)

绘制各阶 GegenbauerC 函数：

绘制 实部：

绘制 虚部：

绘制两个变化参数的实部：

GegenbauerC 函数的类型 2 和 3 有不同的分支切割结构：

函数属性  (14)

整数阶的 GegenbauerC 的域：

整数阶的 GegenbauerC 的范围：

复值的范围是整个平面：

奇阶的 Gegenbauer 多项式是奇数：

偶阶的 Gegenbauer 多项式是偶数：

GegenbauerC 按元素线性作用于列表：

GegenbauerC 具有镜像属性 ：

Gegenbauer 多项式为解析函数：

然而，对于非整数参数而言 GegenbauerC 函数一般不是解析函数：

也不是亚纯函数：

TemplateBox[{2, x}, GegenbauerC2] 既不是非递增，也不是非递减：

TemplateBox[{2, x}, GegenbauerC2] 不是单射函数：

TemplateBox[{2, x}, GegenbauerC2] 不是满射函数：

TemplateBox[{2, x}, GegenbauerC2] 既不是非负，也不是非正：

当 非整数且 时，TemplateBox[{n, x}, GegenbauerC2] 有奇点和断点：

当 为非整数时，TemplateBox[{n, m, x}, GegenbauerC] 有额外的奇点：

TemplateBox[{2, x}, GegenbauerC2] 是凸函数：

TraditionalForm 格式化：

微分  (3)

关于 x 的一阶导：

关于 x 的高阶导：

绘制 n=10，m=1/3 时关于 x 的高阶导数：

关于 x 的 阶导数的公式：

积分  (3)

使用 Integrate 计算不定积分：

验证反导数：

定积分：

更多积分：

级数展开  (2)

使用 Series 求泰勒展开：

绘制 附近的前三个近似：

普通点的泰勒展开：

函数恒等与简化  (4)

GegenbauerC 是 JacobiP 的特殊情况：

GegenbauerC 的导数恒等：

Gegenbauer 多项式的生成函数：

递推关系：

推广和延伸  (2)

将 GegenbauerC 应用到一个幂级数：

GegenbauerC 可以处理实数区间：

应用  (3)

四维拉普拉斯算符的角部分的特征函数：

动量空间表示的氢原子特征函数的径向部分：

在 n 点 Gauss–Lobatto 求积规则中，两个极端节点的值是固定的，而另外 n-2 个节点是通过某个特定的Gegenbauer 多项式的根来计算的. 计算 n 点 Gauss–Lobatto 求积规则的节点和权重：

使用 n 点 Gauss–Lobatto 求积规则来数值计算一个积分：

将 Gauss–Lobatto 求积的结果与 NIntegrate 函数的结果进行比较：

属性和关系  (5)

用 FunctionExpand 将 GegenbauerC 展开成其它函数：

GegenbauerC 可以被表示为 DifferenceRoot：

GegenbauerC 的级数展开的通项

GegenbauerC 的生成函数：

使用 Integrate 定义一个关于函数的内积：

使用 Orthogonalize 构建一个正态基：

该内积生成了 GegenbauerC 多项式：

可能存在的问题  (1)

多项式形式的抵消可能导致不准确的数值结果：

直接计算函数：

Wolfram Research (1988)，GegenbauerC，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GegenbauerC.html （更新于 2022 年）.

文本

Wolfram Research (1988)，GegenbauerC，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GegenbauerC.html （更新于 2022 年）.

CMS

Wolfram 语言. 1988. "GegenbauerC." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2022. https://reference.wolfram.com/language/ref/GegenbauerC.html.

APA

Wolfram 语言. (1988). GegenbauerC. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GegenbauerC.html 年

BibTeX

@misc{reference.wolfram_2024_gegenbauerc, author="Wolfram Research", title="{GegenbauerC}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/GegenbauerC.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gegenbauerc, organization={Wolfram Research}, title={GegenbauerC}, year={2022}, url={https://reference.wolfram.com/language/ref/GegenbauerC.html}, note=[Accessed: 22-November-2024 ]}