GeometricMeanFilter

GeometricMeanFilter[data,r]

filters data by replacing every value by the geometric mean value in its range-r neighborhood.

GeometricMeanFilter[data,{r1,r2,…}]

uses ri for filtering the ^(th)dimension in data.

Details

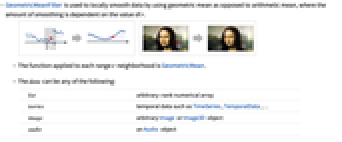
  • GeometricMeanFilter is used to locally smooth data by using geometric mean as opposed to arithmetic mean, where the amount of smoothing is dependent on the value of r.
  • The function applied to each range-r neighborhood is GeometricMean.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries, TemporalData, …
    imagearbitrary Image or Image3D object
    audioan Audio object
  • For multichannel images and audio signals, GeometricMeanFilter operates separately on each channel.
  • GeometricMeanFilter[data,{r1,r2,…}] computes the geometric mean value in 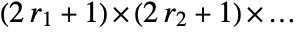blocks centered on each sample.
  • GeometricMeanFilter assumes the index coordinate system for lists and images.
  • At the data boundaries, GeometricMeanFilter uses smaller neighborhoods.

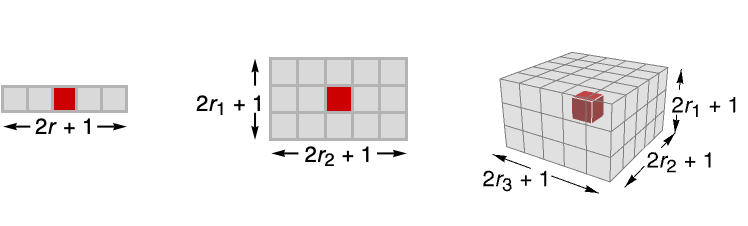
Examples

open allclose all

Basic Examples  (3)

Geometric mean filtering of a list:

Filter a TimeSeries:

Geometric mean filtering of an image:

Scope  (12)

Data  (7)

Apply a moving geometric mean filter to a vector:

Geometric mean filtering of a 2D array:

Filter a quantity array:

Filter an Audio signal:

Filtering a 2D grayscale image:

Geometric mean filtering of a 3D volume:

Filter a symbolic array:

Parameters  (5)

Specify one radius to be used in all directions:

Increasing the radius will result in smoother images:

Geometric mean filtering just in the first direction:

Second direction:

Geometric mean filtering of a 3D image in the vertical direction only:

Filtering of the horizontal planes only:

Use a quantity parameter with a TimeSeries input:

Applications  (3)

Use GeometricMeanFilter to smooth a positive-valued time series and identify the trend:

Reduce noise using geometric mean filtering:

Unsharp masking using geometric mean filtering:

Properties & Relations  (3)

For positive data, HarmonicMeanFilter[data,r]≤GeometricMeanFilter[data,r]≤MeanFilter[data,r]:

Geometric mean filtering is the same as ArrayFilter with function GeometricMean:

Geometric mean filtering is the same as ImageFilter with function GeometricMean:

Wolfram Research (2008), GeometricMeanFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GeometricMeanFilter.html (updated 2016).

Text

Wolfram Research (2008), GeometricMeanFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GeometricMeanFilter.html (updated 2016).

CMS

Wolfram Language. 2008. "GeometricMeanFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GeometricMeanFilter.html.

APA

Wolfram Language. (2008). GeometricMeanFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeometricMeanFilter.html

BibTeX

@misc{reference.wolfram_2025_geometricmeanfilter, author="Wolfram Research", title="{GeometricMeanFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GeometricMeanFilter.html}", note=[Accessed: 22-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_geometricmeanfilter, organization={Wolfram Research}, title={GeometricMeanFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/GeometricMeanFilter.html}, note=[Accessed: 22-March-2025 ]}