Glaisher

Glaisher

is Glaisher's constant with numerical value .

Details

  • Mathematical constant treated as numeric by NumericQ and as a constant by D.
  • Glaisher can be evaluated to any numerical precision using N.
  • Glaisher's constant A satisfies , where is the Riemann zeta function.

Background & Context

  • Glaisher is the symbol representing Glaisher's constant 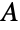, also known as the Glaisher–Kinkelin constant. Glaisher has a number of equivalent definitions throughout mathematics but is most commonly defined as the constant 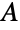that satisfies 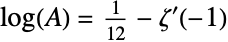, where 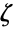is the Riemann zeta function Zeta, 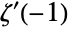is its derivative evaluated at 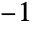, and Log is the natural logarithm. Glaisher has a numerical value 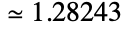. Glaisher arises in mathematical computations including sums, products, and integrals but is especially prominent in sums and integrals involving Gamma and Zeta functions.
  • When Glaisher is used as a symbol, it is propagated as an exact quantity. Expansion and simplification of complicated expressions involving Glaisher may require use of functions such as FunctionExpand and FullSimplify.
  • It is not currently known if Glaisher is rational (meaning it can be expressed as a ratio of integers), algebraic (meaning it is the root of some integer polynomial), or normal (meaning the digits in its base- 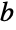expansion are equally distributed) to any base.
  • Glaisher can be evaluated to arbitrary numerical precision using N. However, no efficient formulas for computing large numbers of its digits are currently known. RealDigits can be used to return a list of digits of Glaisher and ContinuedFraction to obtain terms of its continued fraction expansion.

Examples

open allclose all

Basic Examples  (1)

Evaluate to any precision:

Scope  (2)

Do an exact numerical computation:

TraditionalForm formatting:

Applications  (5)

Derivatives of zeta functions:

Integrals containing gamma functions:

Get Glaisher from an infinite product:

Get Glaisher from infinite sums:

Obtains Glaisher from a limit:

Properties & Relations  (1)

Various symbolic relations are automatically used:

Neat Examples  (1)

Terms in the continued fraction:

Wolfram Research (1999), Glaisher, Wolfram Language function, https://reference.wolfram.com/language/ref/Glaisher.html (updated 2007).

Text

Wolfram Research (1999), Glaisher, Wolfram Language function, https://reference.wolfram.com/language/ref/Glaisher.html (updated 2007).

CMS

Wolfram Language. 1999. "Glaisher." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2007. https://reference.wolfram.com/language/ref/Glaisher.html.

APA

Wolfram Language. (1999). Glaisher. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Glaisher.html

BibTeX

@misc{reference.wolfram_2024_glaisher, author="Wolfram Research", title="{Glaisher}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/Glaisher.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_glaisher, organization={Wolfram Research}, title={Glaisher}, year={2007}, url={https://reference.wolfram.com/language/ref/Glaisher.html}, note=[Accessed: 22-December-2024 ]}