GraphDisjointUnion

GraphDisjointUnion[g1,g2]

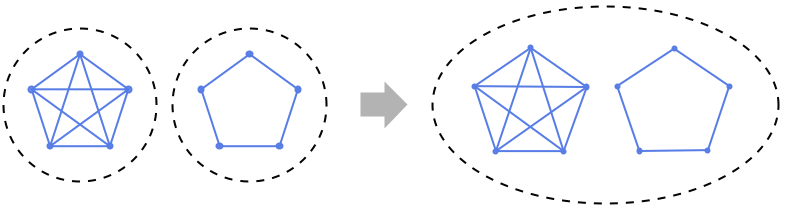
グラフ g1 と g2 のグラフの非交和を与える．

GraphDisjointUnion[g1,g2,…]

g1, g2, …の非交和を与える．

GraphDisjointUnion[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • グラフの非交和はIndexGraph[g1,1]とIndexGraph[g2,n+1]のグラフの和集合で与えられる．n は g1のVertexCountである．
  • GraphDisjointUnionは，無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

予備知識

  • GraphDisjointUnionは，2つ以上の有向グラフあるいは無向グラフによって与えられた新たなグラフを与える．このグラフは，もとの頂点集合および辺集合の和集合を別々に取ることで与えられたものである．GraphDisjointUnionは，異なるグラフ中で同じ頂点ラベルを持つすべての辺を保存するが，頂点には一意的なラベルを付け直す．このため，GraphDisjointUnionは，グラフ理論の専門用語における一般的な意味での「Graph Union」に対応する．結果のグラフは，ラベルが1からもとになっているグラフの頂点数の合計までの，標準的な指標の付いた頂点を持つ．結果のグラフの特定のラベル付けは，もとのグラフの頂点順序とグラフが指定された順序に依存する．この方法でGraphDisjointUnionから得られた，これとは異なるラベルのグラフはすべて同じ同型クラスに属する．
  • 非交和についての隣接行列は，もとのグラフの隣接行列のブロック対角行列に対応する．
  • 関連する関数には，GraphUnion，GraphIntersection，GraphDifferenceがある．GraphDisjointUnionとは異なり，GraphUnionは複数のグラフに同じ頂点ラベルを持つ辺が複数存在する場合は，そのうち1辺のみを保つ．GraphIntersectionは，もとのグラフの頂点集合の和集合と辺集合の交点から得られたグラフを与える．GraphDifferenceは，2つのグラフの頂点集合の和集合と最初のグラフに対する2番目のグラフの辺集合の補集合から得られるグラフを与える．GraphComplementは，与えられたグラフと同じ頂点集合を持つが，もとのグラフには存在しない辺に対応する辺を持つグラフを与える（逆もまた真なり）．

例題

すべて開くすべて閉じる

例  (1)

2つのグラフの非交和を得る：

スコープ  (6)

GraphDisjointUnionは無向グラフに使うことができる：

有向グラフ：

多重グラフ：

混合グラフ：

規則を使ってグラフを指定する：

GraphDisjointUnionは3つ以上のグラフに使うことができる：

特性と関係  (4)

グラフの非交和のVertexCountはグラフの頂点数の合計である：

グラフの非交和のEdgeCountはグラフの辺の合計数である：

グラフの非交和はGraphUnionで求めることができる：

非交和の隣接行列は隣接行列のブロック対角に対応する：

Wolfram Research (2010), GraphDisjointUnion, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDisjointUnion.html （2015年に更新）.

テキスト

Wolfram Research (2010), GraphDisjointUnion, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphDisjointUnion.html （2015年に更新）.

CMS

Wolfram Language. 2010. "GraphDisjointUnion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDisjointUnion.html.

APA

Wolfram Language. (2010). GraphDisjointUnion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDisjointUnion.html

BibTeX

@misc{reference.wolfram_2024_graphdisjointunion, author="Wolfram Research", title="{GraphDisjointUnion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdisjointunion, organization={Wolfram Research}, title={GraphDisjointUnion}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}, note=[Accessed: 24-November-2024 ]}