GraphDisjointUnion

GraphDisjointUnion[g1,g2]

给出图 g1 和 g2 的不相交并集.

GraphDisjointUnion[g1,g2,…]

给出 g1、g2、… 的不相交并集.

GraphDisjointUnion[{vw,…},…]

使用规则 vw 指定图 g.

更多信息和选项

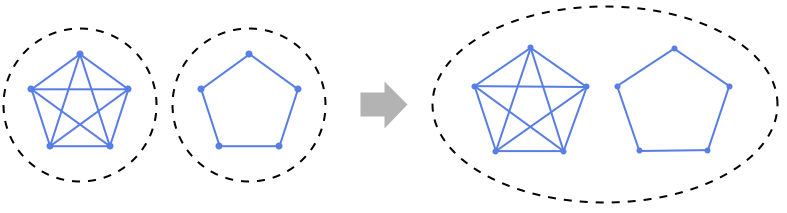
背景

  • GraphDisjointUnion 根据两个或更多个有向或无向图得到一个新图，新图的顶点集和边集分别是原先那些图的顶点集的并集和边集的并集，我们称这个新图为原先这些图的不相交并集. 对不同图中有相同顶点标识的边，GraphDisjointUnion 会把它们全部保留并重命名那些顶点以避免冲突. 因此 GraphDisjointUnion 对应的是图论中通常意义下的“图合并”这一术语. 所得图的顶点具有从 1 开始到初始图顶点总数量的唯一索引. 因此所得图顶点的具体标识可能依赖于原先图中顶点的顺序以及指定那些图时的顺序，不过这样从 GraphDisjointUnion 得到的不同标识的图全都属于同一个同构类.
  • 不相交并集的邻接矩阵对应的是以原先那些矩阵为元素的对角分块矩阵.
  • 和它相关的函数包括 GraphUnion、GraphIntersection 和 GraphDifference. 与 GraphDisjointUnion 不同，若在不同的图中有具备相同顶点标识的多条边那么 GraphUnion 只会保留一条. 对 GraphIntersection 给出的图，其顶点集是原先那些图的顶点集的并集，边集是原先那些图的边集的交集. 对 GraphDifference 给出的图，其顶点集是原先那些图的顶点集的并集，边集是第二个图相对于第一个图的补集. 对 GraphComplement 给出的图，其顶点集和原先的图相同但它的边集则是由原先图缺失的那些边构成（反之也成立）.

范例

打开所有单元关闭所有单元

基本范例  (1)

两个图的不相交并集：

范围  (6)

GraphDisjointUnion 可用于无向图：

有向图：

多重图：

混合图：

使用规则指定图：

GraphDisjointUnion 可用于超过2个图的情况：

属性和关系  (4)

图的不相交并集的 VertexCount 是这些图的总顶点数：

图的不相交并集的 EdgeCount 是这些图的总边数：

图的不相交并集可以使用 GraphUnion 求得：

一个不相交并集的邻接矩阵与邻接矩阵的块对角线相对应：

Wolfram Research (2010)，GraphDisjointUnion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphDisjointUnion.html （更新于 2015 年）.

文本

Wolfram Research (2010)，GraphDisjointUnion，Wolfram 语言函数，https://reference.wolfram.com/language/ref/GraphDisjointUnion.html （更新于 2015 年）.

CMS

Wolfram 语言. 2010. "GraphDisjointUnion." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/GraphDisjointUnion.html.

APA

Wolfram 语言. (2010). GraphDisjointUnion. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GraphDisjointUnion.html 年

BibTeX

@misc{reference.wolfram_2024_graphdisjointunion, author="Wolfram Research", title="{GraphDisjointUnion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}", note=[Accessed: 24-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdisjointunion, organization={Wolfram Research}, title={GraphDisjointUnion}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}, note=[Accessed: 24-November-2024 ]}