Greater

x>y

如果 确实比 大，返回 True.

x1>x2>x3

如果 形成一个严格递增的序列，返回 True.

更多信息

  • Greater 亦称为强不相等或严格不相等.
  • 当 Greater 的参数是实数时，它返回 True 或 False.
  • 当 Greater 的参数不是数时，它会做一些化简.
  • 对于实际的数值，Greater 在内部使用数值近似来建立数值排序. 这个过程会受到全局变量 $MaxExtraPrecision 设置的影响.

范例

打开所有单元关闭所有单元

基本范例  (2)

比较数：

表示一个不等式：

范围  (9)

数值不等式  (7)

仅在实数区域定义不等式：

比较有理数：

至多最后 8 位二进制数不同的近似数被认为是相等的：

比较一个具体的数值表达式和近似数：

比较两个数值表达式；一个数值测试足以证明不等性：

证明不等式需要符号方式：

Greater 使用的符号和数值方法没有足够的精度来反证不等式：

用 RootReduce 来决定代数数的符号：

Greater 使用的数值方法没有足够的精度来证明这个不等式：

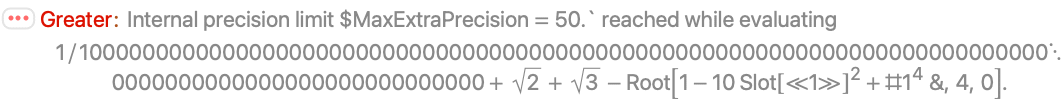
RootReduce 用明确的方法来证明不等性：

增加 $MaxExtraPrecision 可能反证不等性：

符号不等式  (2)

当 x 可能不是一个实数，符号不等式保留不计算形式：

假定 x 是一个实数，用 Refine 重新计算不等式：

一个符号不等式：

用 Reduce 求解集的一个明确的描述：

用 FindInstance 求一个实例：

在不等式定义的区域上用 Minimize 优化：

在不等式定义的假设条件下，用 Refine 化简：

属性和关系  (12)

二元参数的 Greater 的否定形式是 LessEqual：

三元参数的 Greater 的否定形式不能自动化简：

用 LogicalExpand 表示依据二元参数 LessEqual 的否定：

这不等价于三元参数 LessEqual：

当 Greater 不能确定数值表达式间的不等性关系，它保持不计算：

FullSimplify 用明确的符号转换来证明不等性：

Positive[x] 等于 ：

用 Reduce 求解不等式：

用 FindInstance 求一个实例：

用 RegionPlot 和 RegionPlot3D 可视化不等式的解集：

不等式的假设条件：

用 Minimize 和 Maximize 来求解不等式约束条件下的优化问题：

用 NMinimize 和 NMaximize 数值求解约束条件下的优化问题：

在不等式解集上的函数积分：

Median、Quantile 和 Quartiles 用于第 个最大数：

可能存在的问题  (3)

数值精度的近似数的不等式可以是不明确的：

严格的不等式基于额外的数：

任何精度的近似数没有这个问题：

由于自动精度跟踪，Greater 可以仅查看前 10 个数字：

在这个例子中，机器数间的不等式给出预期结果：

在这个例子中，Greater 忽略额外的数字：

Wolfram Research (1988)，Greater，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Greater.html （更新于 1996 年）.

文本

Wolfram Research (1988)，Greater，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Greater.html （更新于 1996 年）.

CMS

Wolfram 语言. 1988. "Greater." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 1996. https://reference.wolfram.com/language/ref/Greater.html.

APA

Wolfram 语言. (1988). Greater. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Greater.html 年

BibTeX

@misc{reference.wolfram_2024_greater, author="Wolfram Research", title="{Greater}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/Greater.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_greater, organization={Wolfram Research}, title={Greater}, year={1996}, url={https://reference.wolfram.com/language/ref/Greater.html}, note=[Accessed: 22-November-2024 ]}