WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

GroupElementToWord
✖
GroupElementToWord

✖

decomposes the group element g as a product of generators of group.

Details and Options

  • The group element g must belong to the given group.
  • GroupElementToWord[group,g] gives the word of g in the form of a list of nonzero integers {m1,…,mk} representing generators in the list returned by GroupGenerators[group]. A positive integer 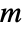in the word represents the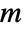 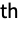^(th) generator, and a negative integer 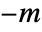represents the inverse of the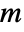 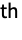^(th) generator.

Examples

open allclose all

Basic Examples  (1)Summary of the most common use cases

Take a permutation g in a group G:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-x6xwq4

Decompose g as a product of generators of G (negative integers represent inverse generators):

In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-8jfeja
Out[2]=2

Reconstruct the permutation from the word:

In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-ecqw64
Out[3]=3

Scope  (2)Survey of the scope of standard use cases

Decompose a permutation as a product of the default generators of a symmetric group:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-no7o4u
Out[1]=1

Decompose the same permutation using a different set of generators for the same group:

In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-ekv0fd
Out[2]=2

The returned words are usually not optimal:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-mx43lr
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-3nki0a
Out[2]=2

This is the optimal solution:

In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-vcehex
Out[3]=3

Check them:

In[4]:=4
✖
https://wolfram.com/xid/0bh1rl67ave8g6-peebsl
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0bh1rl67ave8g6-5rsxg7
Out[5]=5

Options  (3)Common values & functionality for each option

GroupBaseAction  (1)

The algorithm uses a table of coset representatives of the group stabilizers associated to a given base. The choice of this base might strongly affect the resulting word:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-22zrfi
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-x1n8pi
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-6vh573
Out[3]=3

MaxIterations  (1)

Frequently, it is possible to improve the result by allowing the internal algorithm to perform a number of additional iterations:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-7t7rtw
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-wcefme
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-31pkxg
Out[3]=3

Method  (1)

GroupElementToWord uses the Minkwitz algorithm, with a number of parameters:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-nrb04s

Fine-tuning of those parameters may produce shorter words:

In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-zg95dq
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-8ol3dm
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bh1rl67ave8g6-8wwmr8
Out[4]=4

Applications  (1)Sample problems that can be solved with this function

Check that the mapping relating respective generators of these two groups is a homomorphism:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-y0ck2e
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-nomb30

This implements the homomorphism, extending the mapping of generators to all elements:

In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-1rxzsd

Check that for any two elements of G1, the homomorphism property is obeyed:

In[4]:=4
✖
https://wolfram.com/xid/0bh1rl67ave8g6-2tqsr0
Out[4]=4

In this case, the homomorphism is actually an isomorphism:

In[5]:=5
✖
https://wolfram.com/xid/0bh1rl67ave8g6-xcgtqc
Out[5]=5

Properties & Relations  (4)Properties of the function, and connections to other functions

GroupElementFromWord reconstructs the original group element from the word:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-nyzdbe
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-mthje3
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-kaziv6
Out[3]=3

Identity generators are not used, but affect the indexing of the other generators:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-ddkd6y
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-p102vq
Out[2]=2

The identity permutation always corresponds to the empty word:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-usl45d
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-t2x56s
Out[2]=2

The element must belong to the group:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-0p7u1y
In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-vttua4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-2q35dz
Out[3]=3

Neat Examples  (1)Surprising or curious use cases

The group of a 3×3×3 Rubik's cube is usually given in terms of six generators:

In[1]:=1
✖
https://wolfram.com/xid/0bh1rl67ave8g6-hg7msy

However, one of them is redundant, and the group can actually be constructed with only five face rotations:

In[2]:=2
✖
https://wolfram.com/xid/0bh1rl67ave8g6-rf98hl
In[3]:=3
✖
https://wolfram.com/xid/0bh1rl67ave8g6-va30ep
Out[3]=3

This is a possible word expressing the sixth rotation in terms of the first five and their inverses:

In[4]:=4
✖
https://wolfram.com/xid/0bh1rl67ave8g6-tohcf0
Out[4]=4

Check it:

In[5]:=5
✖
https://wolfram.com/xid/0bh1rl67ave8g6-rcwl13
Out[5]=5

After removing the generators corresponding to opposite faces, the remaining four still move all facelets, but now they only generate a subgroup of index 2048:

In[6]:=6
✖
https://wolfram.com/xid/0bh1rl67ave8g6-vex555
In[7]:=7
✖
https://wolfram.com/xid/0bh1rl67ave8g6-5pvhws
Out[7]=7

This is because there are two disconnected sets of edge facelets:

In[8]:=8
✖
https://wolfram.com/xid/0bh1rl67ave8g6-btjr43
Out[8]=8

Compare with the original situation:

In[9]:=9
✖
https://wolfram.com/xid/0bh1rl67ave8g6-fhrrmg
Out[9]=9
Wolfram Research (2012), GroupElementToWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementToWord.html.
✖
Wolfram Research (2012), GroupElementToWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementToWord.html.

Text

Wolfram Research (2012), GroupElementToWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementToWord.html.

✖
Wolfram Research (2012), GroupElementToWord, Wolfram Language function, https://reference.wolfram.com/language/ref/GroupElementToWord.html.

CMS

Wolfram Language. 2012. "GroupElementToWord." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GroupElementToWord.html.

✖
Wolfram Language. 2012. "GroupElementToWord." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GroupElementToWord.html.

APA

Wolfram Language. (2012). GroupElementToWord. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GroupElementToWord.html

✖
Wolfram Language. (2012). GroupElementToWord. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GroupElementToWord.html

BibTeX

@misc{reference.wolfram_2025_groupelementtoword, author="Wolfram Research", title="{GroupElementToWord}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GroupElementToWord.html}", note=[Accessed: 29-March-2025 ]}

✖
@misc{reference.wolfram_2025_groupelementtoword, author="Wolfram Research", title="{GroupElementToWord}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GroupElementToWord.html}", note=[Accessed: 29-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_groupelementtoword, organization={Wolfram Research}, title={GroupElementToWord}, year={2012}, url={https://reference.wolfram.com/language/ref/GroupElementToWord.html}, note=[Accessed: 29-March-2025 ]}

✖
@online{reference.wolfram_2025_groupelementtoword, organization={Wolfram Research}, title={GroupElementToWord}, year={2012}, url={https://reference.wolfram.com/language/ref/GroupElementToWord.html}, note=[Accessed: 29-March-2025 ]}