GroupElementToWord

GroupElementToWord[group,g]

群の元 g を group の生成元の積として分解する．

詳細とオプション

  • 群の元 g は指定の群に属さなければならない．
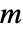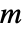
  • GroupElementToWord[group,g]は g の語を，GroupGenerators[group]で返されるリスト中の生成元を表す非零の整数のリスト{m1,…,mk}の形で与える．語中の正の整数 は第 生成元を表し，負の整数 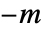は第 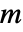生成元の逆を表す．

例題

すべて開くすべて閉じる

例  (1)

群 G 中の置換 g を取る：

g を G の生成元の積として分解する（負の整数は逆生成元を表す）：

語から置換を再構築する：

スコープ  (2)

置換を対称群のデフォルトの生成元の積として分解する：

同じ置換を同じ群の異なる生成元集合を使って分解する：

返された語は大抵の場合最適化されていない：

これは最適解である：

これらを確かめる：

オプション  (3)

GroupBaseAction  (1)

このアルゴリズムは与えられた基底に関連し固定群の剰余類代表の表を使う．この基底の選択が結果の語に大きく影響するかもしれない：

MaxIterations  (1)

しばしば，内部アルゴリズムを使って多数の追加的な反復を行うことで結果を向上させることができる：

Method  (1)

GroupElementToWordは多くのパラメータと共にMinkwitzアルゴリズムを使う：

これらのパラメータを微調整すると語が短くなるかもしれない：

アプリケーション  (1)

この2つの群のそれぞれの生成元に関連するマッピングが準同型であることを確かめる：

これは，生成元のマッピングをすべての元に拡張することで準同型性を実装する：

G1の任意の2つの元が準同型特性に従っていることを確かめる：

この場合，準同型は実際は同型である：

特性と関係  (4)

GroupElementFromWordは語からもとの群の元を再構築する：

恒等生成元は使われないが，他の生成元の指標に影響する：

恒等置換は常に空の語に相当する：

元は群に属さなければならない：

おもしろい例題  (1)

3×3×3のルービックキューブの群は通常6つの生成元で与えられる：

しかし，そのうちの一つは冗長であり，群は実際は5つの面の循環で構築することができる：

これは最初の5つとその逆によって6番目の循環を表す可能な語である：

これを検証する：

反対の面に相当する生成元を削除した後，残りの4つの生成元はまだすべてのフェイスレットを動かせるが，指標2048の部分群しか生成できなくなっている：

これは，2組の辺のフェイスレットが未結合であるからである：

もとの状況と比較する：

Wolfram Research (2012), GroupElementToWord, Wolfram言語関数， https://reference.wolfram.com/language/ref/GroupElementToWord.html.

テキスト

Wolfram Research (2012), GroupElementToWord, Wolfram言語関数， https://reference.wolfram.com/language/ref/GroupElementToWord.html.

CMS

Wolfram Language. 2012. "GroupElementToWord." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GroupElementToWord.html.

APA

Wolfram Language. (2012). GroupElementToWord. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GroupElementToWord.html

BibTeX

@misc{reference.wolfram_2024_groupelementtoword, author="Wolfram Research", title="{GroupElementToWord}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GroupElementToWord.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_groupelementtoword, organization={Wolfram Research}, title={GroupElementToWord}, year={2012}, url={https://reference.wolfram.com/language/ref/GroupElementToWord.html}, note=[Accessed: 18-November-2024 ]}