HaarWavelet
表示一个哈尔小波.
更多信息

- HaarWavelet 定义了一个正交小波族.
- 尺度函数(
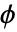 )与小波函数(
)与小波函数(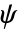 )具有长度为 1 的紧支集. 它们具有一个消失矩,且对称.
)具有长度为 1 的紧支集. 它们具有一个消失矩,且对称. - 尺度函数(
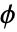 )为
)为 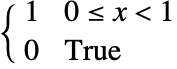 . »
. » - 小波函数(
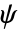 )为
)为 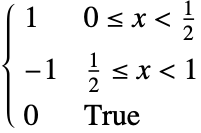 . »
. » - HaarWavelet 可与诸如 DiscreteWaveletTransform、WaveletPhi 等函数联合使用.
范例
打开所有单元关闭所有单元范围 (10)
小波变换 (5)
HaarWavelet 可被用于进行 DiscreteWaveletPacketTransform:
HaarWavelet 可被用于进行 StationaryWaveletTransform:
HaarWavelet 可被用于进行 StationaryWaveletPacketTransform:
HaarWavelet 可被用于进行 LiftingWaveletTransform:
属性和关系 (15)
DaubechiesWavelet[1] 等价于 HaarWavelet:
HaarWavelet 具有一个消失矩;![]() :
:
Wolfram Research (2010),HaarWavelet,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HaarWavelet.html.
文本
Wolfram Research (2010),HaarWavelet,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HaarWavelet.html.
CMS
Wolfram 语言. 2010. "HaarWavelet." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HaarWavelet.html.
APA
Wolfram 语言. (2010). HaarWavelet. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HaarWavelet.html 年