HjorthDistribution
HjorthDistribution[m,s,f]
表示 Hjorth 分布,其位置参数为 m,尺度参数为 s,形状参数为 f.
更多信息

- 可将 HjorthDistribution 用于模拟不同类型的故障,进行可靠性分析.
- Hjorth 分布中值
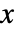 的存活函数为:
的存活函数为: 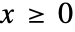 时,为
时,为 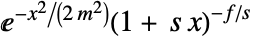 ,其他情况下为
,其他情况下为 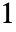 .
. - HjorthDistribution[m,s,f] 允许 m 和 s 为任意正实数,f 为任意非负实数.
- HjorthDistribution[m,s,f] 允许 m、s 和 f 为使得 m*s 和 m*f 无量纲的任意量. »
- HjorthDistribution 可与诸如 Mean、CDF 和 RandomVariate 这样的函数一起使用.
范例
打开所有单元关闭所有单元范围 (6)
在参数中使用 Quantity 时保持一致性会产生 QuantityDistribution:
应用 (5)
设备的寿命服从 HjorthDistribution. 求设备的可靠性:
可用参数为 ![]() 、
、![]() 和
和 ![]() 的 HjorthDistribution 来描述一个元件的失效行为. 求元件在第一年失效的概率:
的 HjorthDistribution 来描述一个元件的失效行为. 求元件在第一年失效的概率:
由于生产时质量参差不齐,一个电子设备的初始故障率很高. 可用参数为 ![]() 、
、![]() 和
和 ![]() 的 HjorthDistribution 来模拟它的寿命. 绘制风险函数:
的 HjorthDistribution 来模拟它的寿命. 绘制风险函数:
为了避免过早失效的情况,在“试机”阶段以超负荷水平运行设备. 计算在多长的试机阶段后第一年的失效率可以降低一半:
一个简单的机械系统由三个独立的元件组成:两个 A 型元件和一个 B 型元件. 测得的失效时间(单位为天数)为:
求两种元件的估计分布,假定它们服从 HjorthDistribution:
每种元件中只要有一个能正常工作系统就可以运行. 计算系统的可靠性:
一个简单的机械系统由三个独立的元件组成:两个 A 型元件和一个 B 型元件. 每种元件中只要有一个能正常工作系统就可以运行. 每种类型的元件的失效时间服从下列分布:
属性和关系 (5)
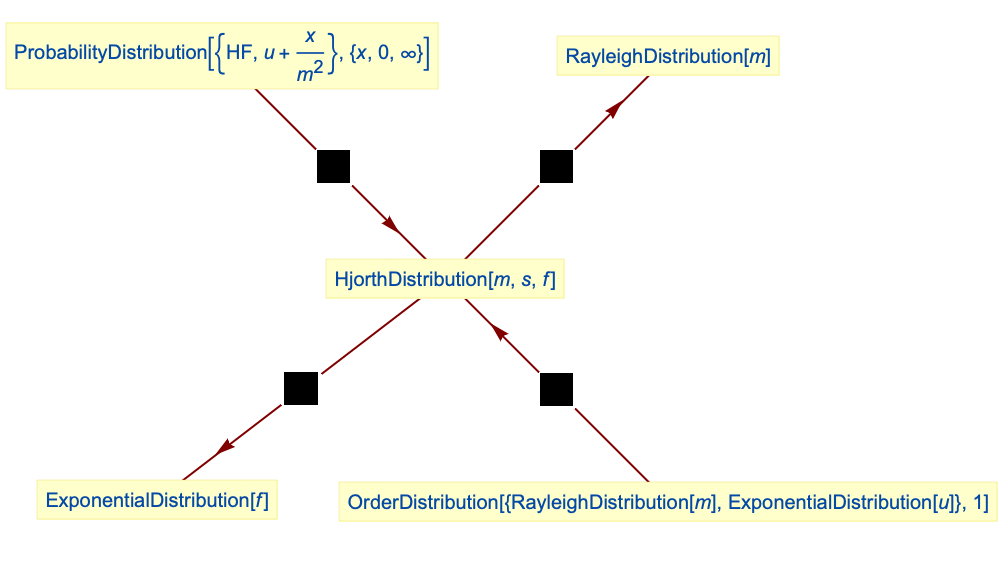
Hjorth 分布可被简化为 RayleighDistribution:
可以通过初始失效率服从 GammaDistribution 的线性风险率分布的 ParameterMixtureDistribution 获得 Hjorth 分布:
可以通过 ExponentialDistribution 和 RayleighDistribution 的 OrderDistribution 获得线性风险率分布:
ExponentialDistribution 是 Hjorth 分布的极限情况:
可能存在的问题 (5)
HjorthDistribution 在 m 或 s 不为正实数的情况下没有定义:
HjorthDistribution 在 f 为非负实数的情况下没有定义:
文本
Wolfram Research (2017),HjorthDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HjorthDistribution.html.
CMS
Wolfram 语言. 2017. "HjorthDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HjorthDistribution.html.
APA
Wolfram 语言. (2017). HjorthDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HjorthDistribution.html 年