ReliabilityDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
represents the reliability distribution for a system with components xi having reliability distribution disti, where the whole system is working when the Boolean expression bexpr is True, and component xi is working when xi is True.


ReliabilityDistribution
ReliabilityDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
represents the reliability distribution for a system with components xi having reliability distribution disti, where the whole system is working when the Boolean expression bexpr is True, and component xi is working when xi is True.
Details

- ReliabilityDistribution[bexpr,…] corresponds to a reliability block diagram specification.
- The Boolean expression bexpr is also known as the structure function for the system.
- Typical structure functions include:
-
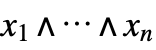
series system 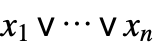
parallel system ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/ReliabilityDistribution.en/3.png)
k-out-of-n system BooleanConsecutiveFunction[k,n] consecutive-k-out-of-n system - The structure function bexpr can be any positive unate Boolean function.
- UnateQ[bexpr] can be used to test whether a Boolean expression is positive unate.
- The component reliability distributions disti need to be univariate with PDF[disti,t] zero for t≤0.
- For ReliabilityDistribution[bexpr,…] with component indicator variables xi:
-
xiTrue indicates component xi working xiFalse indicates component xi failed - The survival function at time t for ReliabilityDistribution[bexpr,{{x1,dist1},…}] is given by Probability[bexpr/.{x1->t1>t,…},{t1disti,…}].
- ReliabilityDistribution can be used with such functions as Mean, SurvivalFunction, HazardFunction, and RandomVariate.
Examples
open all close allBasic Examples (3)
Scope (26)
Basic Uses (4)
Find the mean time to failure for a parallel system with two components:
Find the SurvivalFunction of a system that needs two out of three components to work:
Find the mean time to failure (MTTF) for a serial system with one standby component:
Structure Functions (7)
A system with two components in series with two in parallel:
A system with three components and a voting gate:
A system that works if at least three out of four components work:
Any positive unate Boolean expression can be used as a structure function:
Use UnateQ to test whether a Boolean expression is positive unate:
Construct a multi-stage system, where each component is a ![]() -out-of-
-out-of-![]() system:
system:
A redundant consecutive ![]() -out-of-
-out-of-![]() with redundancy in each consecutive structure component:
with redundancy in each consecutive structure component:
Parametric Lifetime Distributions (5)
A system with an increasing and decreasing failure rate:
Use any parametric lifetime distribution including LogNormalDistribution:
Numerically compute the mean time to failure:
Compute the mean time to failure as a function of distribution parameters:
When one component has a substantially longer lifetime, it determines the system lifetime:
Define two distributions with the same mean time to failure:
Define a parallel and serial system with these distributions:
Show how the different mean times to failure vary with ![]() :
:
Discrete lifetime distributions can be used:
Calculate the mean time to failure:
Plot the SurvivalFunction:
Nonparametric Lifetime Distributions (3)
Model airplane glass strength using SmoothKernelDistribution:
Consider a series-connected system with one component being airplane glass:
Model components with a HistogramDistribution:
Plot the survival function for a serial system with two and three components:
Model components directly from data with EmpiricalDistribution:
Plot the survival function for a parallel system with two components:
Derived Lifetime Distributions (7)
Model a component with a StandbyDistribution:
Calculate the mean time to failure:
Plot the SurvivalFunction:
Complex systems can be modeled in steps:
Find the mean time to failure:
This is equivalent to modeling the whole system at once:
Model a component with a StandbyDistribution:
Both components need to work for the system to work:
Plot the survival function and compare with only the standby component:
A system with a ParameterMixtureDistribution:
Model a two-component cold standby system with a MixtureDistribution:
Use it in ReliabilityDistribution and compute the survival function:
Show equivalence with StandbyDistribution:
OrderDistribution can be used to model component lifetimes:
Plot the SurvivalFunction:
MarginalDistribution can be used to model component lifetimes:
Plot the SurvivalFunction:
Applications (12)
Model the launch of an aircraft. The hangar door can be opened electronically or manually:
Two fuel pumps require power to run:
Two more pumps run on reliable batteries, giving the following fuel transfer structure:
Also needed is deicing of the aircraft and a fuel storage tank:
Define distributions with failure rates per hour. Let the failure rate of the power supply be variable:
Compute the survival function and the mean:
Study how the reliability varies when the failure rate ![]() is decreased from
is decreased from ![]() /hour:
/hour:
A vacuum system in a small electron accelerator contains 20 vacuum bulbs arranged in a circle. The vacuum system fails if at least three adjacent vacuum bulbs fail:
Compute the mean time to failure:
A satellite needs power from its battery, which is recharged by solar panels. Calculate the number of load cycles the system can stand:
The battery has a standby battery:
Simulate the number of load cycles the satellite can manage:
Consider a skateboard with a ball bearing in each of its wheels. Find out the lifetime of such a skateboard:
Model the ball bearings with a known distribution:
Assume the skateboard can be used when at least three out of four wheels are functioning:
A car has four tires that are all needed to drive. Given the lifetime distribution of a tire as ExponentialDistribution[0.0004], calculate the failure rate and mean time to failure (MTTF) of the car with respect to the tires:
Simulate the lifetime of the car:
In order to fly, an airplane needs both wings, one engine out of two on each wing, and the air control system operating. Model the engine system:
Calculate the mean time to failure for the airplane:
Calculate the probability that a six-hour flight will be successful:
Find the probability that an airplane working after 300 hours still works after an additional 200 hours:
Simulate the lifetime of the airplane:
A data center needs 20 servers to work, one power supply, one cooling system, and one network connection. The power supply has a standby component. The network connection consists of two parallel connections. Model the server:
Model the power supply with StandbyDistribution:
Calculate the mean time to failure (MTTF):
Simulate the uptime of the data center:
Find the component that is most important to improve in a single server:
A system has the following structure and lifetime distribution:
Find the requirement on the failure rate ![]() to survive a mission of five days with a probability of 0.9995:
to survive a mission of five days with a probability of 0.9995:
A solar panel consists of arrays of photovoltaic cells. Each array has 10 cells:
The solar panel requires three out of five arrays and an inverter to work:
Find the mean time to failure in years:
Simulate the lifetimes of solar panels:
A company that sells solar panels gives a 10-year warranty. An additional 10 years can be added. Find out how the company should price this extended warranty:
A logistics company uses trucks, a ship, and a train to deliver goods to customers. Two out of three trucks and clear roads are needed for road transport. A working ship and calm weather conditions are needed for the ship, and a functioning train and tracks are needed for the train. Model the road transport:
Calculate the expected number of days before the system fails to deliver to the customers:
The company is considering leasing an airplane to improve the reliability of delivery. Calculate how much this airplane would improve the mean time to failure:
Assume that Charles Lindbergh had the option to select a one-engine or a two-engine aircraft for his flight between New York and Paris. Investigate which configuration of engines gives the highest reliability:
Plot the survival functions for these different configurations:
It is clear that the best choice was two engines in parallel, which at the time was not available, and Lindbergh therefore chose one engine. Calculate the probability that one engine survives a 33.5-hour flight:
Model a launch into space in three phases: a ground check, a launch phase, and in orbit. Define the lifetime distributions for operating and inactive modes:
For the ground phase, an environmental accelerator of 5 is used:
The launch phase presents a harsher environment, with the environmental factor 400:
The environment in orbit is not very harsh, so a factor 1 is used:
If the ground check takes 24 hours, the launch 0.1 hours, and the orbit phase 100 days, find the probability of success:
Properties & Relations (14)
ReliabilityDistribution uses local names for variables in the input:
Hence, subsequent computations can be done with the original variable name:
The probability that two components both have a lifetime greater than ![]() :
:
This corresponds to a series connection:
The probability that at least one component has a lifetime greater than ![]() :
:
This corresponds to a parallel connection:
The probability that at least two components have a lifetime greater than ![]() :
:
This corresponds to a 2-out-of-3 system:
A series connection of identical components corresponds to an OrderDistribution:
A parallel connection of identical components corresponds to an OrderDistribution:
The lifetime of a series connected system is the minimum of the component lifetimes:
The lifetime of a parallel connected system is the maximum of the component lifetimes:
A ![]() -out-of-
-out-of-![]() system corresponds to a TransformedDistribution with a RankedMin function:
system corresponds to a TransformedDistribution with a RankedMin function:
Compare the survival functions:
A series system of exponentially distributed components is exponential:
A series system of components with a Weibull lifetime distribution is another Weibull:
ReliabilityDistribution models that component ![]() or
or ![]() has to work for the system to work:
has to work for the system to work:
The corresponding FailureDistribution models the events that both ![]() and
and ![]() fail:
fail:
Component ![]() or
or ![]() working is equivalent to the event of both
working is equivalent to the event of both ![]() and
and ![]() failing:
failing:
Model two out of four components needing to work for the system to work:
This is equal to three out of four components needing to fail for the system to fail:
ReliabilityDistribution[f[x1,…],…]FailureDistribution[¬f[¬x1,…],…]:
Retrieve the ReliabilityDistribution for a SystemModel with reliability information:
Possible Issues (3)
Component distributions need to have a positive domain:
Use TruncatedDistribution to restrict the domain to positive values only:
Exact or symbolic properties cannot always be computed:
Approximate values can typically still be found:
A ReliabilityDistribution is only well defined for positive unate structure expressions:
Use UnateQ to test whether a Boolean expression is positive unate:
Neat Examples (2)
Show the hazard function for all systems with up to four identical components:
Build list of unique hazard functions:
Plot hazard functions and corresponding systems:
Use a Graph as a reliability block diagram:
Calculate the mean time to failure with the green and red vertices as the start and end vertices:
History
Text
Wolfram Research (2012), ReliabilityDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
CMS
Wolfram Language. 2012. "ReliabilityDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ReliabilityDistribution.html.
APA
Wolfram Language. (2012). ReliabilityDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ReliabilityDistribution.html
BibTeX
@misc{reference.wolfram_2025_reliabilitydistribution, author="Wolfram Research", title="{ReliabilityDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ReliabilityDistribution.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_reliabilitydistribution, organization={Wolfram Research}, title={ReliabilityDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/ReliabilityDistribution.html}, note=[Accessed: 10-March-2026]}