IntegrateChangeVariables

IntegrateChangeVariables[integral,u,trans]

changes the variable in integral to the new variable u using the transformation trans.

IntegrateChangeVariables[integral,{u,v,…},trans]

changes the variables to the new variables u, v, ….

Details and Options

  • IntegrateChangeVariables is also known as integration by substitution, u-substitution and reverse chain rule.
  • A change of variables is often used in calculus to simplify an integral by applying a suitable substitution to it or by representing it in another coordinate system to exploit the symmetry in the problem.
  • IntegrateChangeVariables can be used to perform a change of variables for indefinite integrals, definite integrals, multiple integrals and integrals over geometric regions.
  • The change of variables is performed using the change of variables formula
  • on an interval 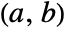or
  • over a region 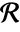where 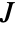denotes the Jacobian of the transformati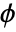on on .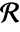
  • The possible forms for integral are the forms supported by Integrate:
  • Integrate[f[x],x]indefinite univariate integral
    Integrate[f[x],{x,a,b}]definite univariate integral
    Integrate[f[x,y,…],x,y,…]indefinite multivariate integral
    Integrate[f[x,y,…],{x,a,b},{y,c,d},…]definite multivariate integral
    Integrate[f[x,y,…],{x,y,…}∈reg]definite multivariate integral over a region
  • Either an unevaluated Integrate[…] or Inactive[Integrate][…] can be used. It is important that the integral does not evaluate, so the safe method is to use Inactive[Integrate][…] which can be produced through Inactivate[integral,Integrate].
  • IntegrateChangeVariables returns the result in the form Inactive[Integrate][…]. Use Activate to evaluate the integral in the new coordinates. »
  • The transformation trans can have the forms:
  • t==ϕ[x]replace ϕ[x] by t
    {u==ϕ[x,y,…],v==ψ[x,y,…],…}replace ϕ[x,y,…] by u and ψ[x,y,…] by v, etc.
    chart1chart2named coordinate systems from CoordinateChartData
  • The transformation 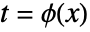is assumed to be differentiable on its domain of definition.
  • When using named coordinate systems, the transformation can be entered in any form accepted by CoordinateTransformData, including {oldsys,metric,dim}{newsys,metric,dim}, {oldsysnewsys,metric,dim} and the various more abbreviated forms.
  • Restrictions on the domains of the variables and parameters in the integral can be specified using Assumptions.

Examples

open allclose all

Basic Examples  (4)

Apply the change of variables to an indefinite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Create an inactive multiple integral:

Apply a change of variables to the multiple integral:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to an approximation of a multiple integral:

Evaluate the result:

Compare the result with the original approximation of the multiple integral:

Scope  (21)

Indefinite Integrals  (5)

Apply the change of variables to an indefinite integral:

The transformation can be given with the old variables in terms of the new ones, :

Evaluate the result and substitute back to the original variables:

Compare the result with the original integral:

Apply the change of variables to an indefinite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to an indefinite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables and to an indefinite multiple integral:

Evaluate the result:

Compare the result with the original integral:

Change an indefinite integral from Cartesian to planar parabolic coordinates:

Definite Integrals  (6)

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Apply the change of variables to a definite integral:

Evaluate the result:

Compare the result with the original integral:

Multiple Integrals  (8)

Apply a change of variables to a multiple integral:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to a multiple integral:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to a multiple integral:

Evaluate the result:

The numerical value of the above result agrees with the result returned by NIntegrate:

Apply a change of variables to a multiple integral:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to a multiple integral:

Evaluate the result:

Apply a change of variables to a multiple integral:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to a multiple integral:

Evaluate the result:

Apply a change of variables to a multiple integral:

Evaluate the result:

Compare the result with the original integral:

Integrals over Regions  (2)

Apply the change of variables and to a multiple integral over a region:

Evaluate the result:

Compare the result with the original integral:

Apply a change of variables to a multiple integral over a region:

Evaluate the result:

Compare the result with the original integral:

Applications  (4)

Compute the area of the annulus:

The area of the annulus could also be represented by the following integral, agreeing with the result above:

Evaluate the result:

Compute the area of the following region:

The area of the region is represented by the following integral:

The region is transformed into the following square with the transformation and :

Evaluate the result:

Attempt to compute the following definite integral; it takes a long time and only partially evaluates:

Changing to polar coordinates gives a much simpler integral to evaluate:

The numerical value of the above result agrees with the result returned by NIntegrate:

Attempt to compute the following definite integral; it takes a long time and only partially evaluates:

Changing to polar coordinates gives a much simpler integral to evaluate:

The numerical value of the above result agrees with the result returned by NIntegrate:

Properties & Relations  (2)

A result always has an inactive head, irrespective of the form of input:

Use Activate to evaluate the integral:

IntegrateChangeVariables uses information from both CoordinateChartData and CoordinateTransformData:

The foregoing used both the mapping and the coordinate ranges to give as simple a result as possible:

Wolfram Research (2022), IntegrateChangeVariables, Wolfram Language function, https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

Text

Wolfram Research (2022), IntegrateChangeVariables, Wolfram Language function, https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

CMS

Wolfram Language. 2022. "IntegrateChangeVariables." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html.

APA

Wolfram Language. (2022). IntegrateChangeVariables. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html

BibTeX

@misc{reference.wolfram_2025_integratechangevariables, author="Wolfram Research", title="{IntegrateChangeVariables}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html}", note=[Accessed: 18-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_integratechangevariables, organization={Wolfram Research}, title={IntegrateChangeVariables}, year={2022}, url={https://reference.wolfram.com/language/ref/IntegrateChangeVariables.html}, note=[Accessed: 18-February-2025 ]}