InverseWishartMatrixDistribution[ν,Σ]
represents an inverse Wishart matrix distribution with ν degrees of freedom and covariance matrix Σ.


InverseWishartMatrixDistribution
InverseWishartMatrixDistribution[ν,Σ]
represents an inverse Wishart matrix distribution with ν degrees of freedom and covariance matrix Σ.
Details
- The probability density for a symmetric matrix
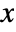 in an inverse Wishart matrix distribution is proportional to
in an inverse Wishart matrix distribution is proportional to 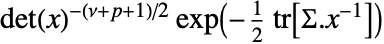 , where
, where 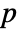 is the size of matrix Σ.
is the size of matrix Σ. - For a matrix
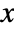 distributed as InverseWishartMatrixDistribution[ν,Σ], the inverse
distributed as InverseWishartMatrixDistribution[ν,Σ], the inverse 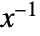 is distributed as WishartMatrixDistribution[ν,Σ-1].
is distributed as WishartMatrixDistribution[ν,Σ-1]. - The covariance matrix
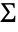 can be any positive definite symmetric matrix of dimensions
can be any positive definite symmetric matrix of dimensions  and ν can be any real number greater than
and ν can be any real number greater than 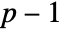 .
. - InverseWishartMatrixDistribution can be used with such functions as MatrixPropertyDistribution, EstimatedDistribution, and RandomVariate.
Examples
open all close allBasic Examples (3)
Generate a pseudorandom matrix:
Check that it is positive definite:
Sample eigenvalues of an inverse Wishart random matrix using MatrixPropertyDistribution:
Scope (6)
Generate a single pseudorandom matrix:
Generate a set of pseudorandom matrices:
Compute statistical properties numerically:
Numerically approximate expectation of the largest matrix eigenvalue ![]() :
:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare LogLikelihood for both distributions:
Properties & Relations (3)
![]() , where
, where ![]() and
and ![]() are independent Gaussian vector and Wishart matrix follows HotellingTSquareDistribution:
are independent Gaussian vector and Wishart matrix follows HotellingTSquareDistribution:
Use MatrixPropertyDistribution to sample expressions ![]() :
:
Any diagonal element of inverse Wishart random matrix follows scaled inverse χ2 distribution:
Diagonal elements are not independent:
For any nonzero vector ![]() and inverse Wishart matrix
and inverse Wishart matrix ![]() with scale matrix
with scale matrix ![]() ,
, ![]() is χ2 distributed:
is χ2 distributed:
Related Guides
Text
Wolfram Research (2015), InverseWishartMatrixDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html (updated 2017).
CMS
Wolfram Language. 2015. "InverseWishartMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html.
APA
Wolfram Language. (2015). InverseWishartMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html
BibTeX
@misc{reference.wolfram_2025_inversewishartmatrixdistribution, author="Wolfram Research", title="{InverseWishartMatrixDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html}", note=[Accessed: 12-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_inversewishartmatrixdistribution, organization={Wolfram Research}, title={InverseWishartMatrixDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html}, note=[Accessed: 12-January-2026]}