MatrixNormalDistribution[Σrow,Σcol]
represents a zero mean matrix normal distribution with row covariance matrix Σrow and column covariance matrix Σcol.
MatrixNormalDistribution[μ,Σrow,Σcol]
represents a matrix normal distribution with mean matrix μ.


MatrixNormalDistribution
MatrixNormalDistribution[Σrow,Σcol]
represents a zero mean matrix normal distribution with row covariance matrix Σrow and column covariance matrix Σcol.
MatrixNormalDistribution[μ,Σrow,Σcol]
represents a matrix normal distribution with mean matrix μ.
Details

- MatrixNormalDistribution is a distribution of μ+
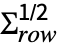 .x.
.x.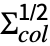 , where
, where 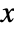 is a matrix with independent identically distributed matrix elements that follow NormalDistribution[0,1].
is a matrix with independent identically distributed matrix elements that follow NormalDistribution[0,1]. - The probability density for a matrix
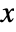 in a matrix normal distribution is proportional to
in a matrix normal distribution is proportional to 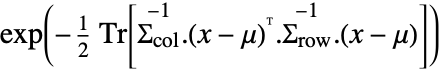 .
. - MatrixNormalDistribution[μ,c Σrow,c-1 Σcol] has the same distribution as MatrixNormalDistribution[μ,Σrow,Σcol] for any positive real constant c.
- The covariance matrices Σrow and Σcol can be any symmetric positive definite matrices of real numbers of dimensions {n,n} and {m,m}, respectively, and the mean matrix μ can be any matrix of real numbers of dimensions {n,m}.
- MatrixNormalDistribution can be used with such functions as MatrixPropertyDistribution, EstimatedDistribution, and RandomVariate.
Examples
open all close allScope (7)
Generate a single pseudorandom matrix:
Generate a single pseudorandom matrix with nonzero mean:
Generate a set of pseudorandom matrices:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare LogLikelihood for both distributions:
Find the probability that the smallest eigenvalue ![]() :
:
Applications (2)
Visualize sample matrices from matrix normal distributions:
Use a matrix normal distribution to simulate a vector autoregressive process:
Construct TemporalData from sampled values:
Properties & Relations (6)
A matrix normal distribution is defined up to a positive multiplicative constant:
Equivalent distribution with row and column scale matrices multiplied and divided by a positive constant:
Compute the PDF of the distributions at a random point:
MatrixTDistribution[Σrow,Σcol,ν] is a parameter mixture of MatrixNormalDistribution[Σ,Σcol] with ![]() following InverseWishartMatrixDistribution[ν+n-1,Σrow]:
following InverseWishartMatrixDistribution[ν+n-1,Σrow]:
Create a sample following the parameter mixture of MatrixNormalDistribution with InverseWishartMatrixDistribution:
Fit the sample data to MatrixTDistribution:
Compute log-likelihood ratio statistic against the appropriate MatrixTDistribution:
Log-likelihood ratio follows ChiSquareDistribution with the parameter equal to the number of degrees of freedom:
Compute the ![]() -value of log-likelihood ratio test:
-value of log-likelihood ratio test:
Sample from a matrix normal distribution with independent rows:
Test the hypothesis that rows follow a multinormal distribution with the column covariance matrix:
Sample from a matrix normal distribution with independent rows:
Test the hypothesis that rows follow a multinormal distribution with the column covariance matrix:
Sample from a matrix normal distribution with independent rows:
Computing sample inter-row covariances shows different rows are pairwise independent:
Computing sample inter-column covariances shows different columns are dependent:
By joining the rows of the matrix-valued random variable together, a matrix normal distribution can be regarded as a multivariate normal distribution:
The covariance matrix of the vectorized random matrix is the Kronecker product of ![]() and
and ![]() :
:
Possible Issues (1)
A matrix normal distribution is defined up to a multiplicative scaling constant. The estimated parameters may not be close to the ones that specify the underlying distribution:
Sample from the matrix normal distribution:
Compare the estimated scale parameters with the ones of the underlying distribution:
Kronecker products of the scale matrices are close to each other:
The LogLikelihood of the distribution indicates that the estimate is good:
Related Guides
Text
Wolfram Research (2015), MatrixNormalDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixNormalDistribution.html (updated 2017).
CMS
Wolfram Language. 2015. "MatrixNormalDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/MatrixNormalDistribution.html.
APA
Wolfram Language. (2015). MatrixNormalDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixNormalDistribution.html
BibTeX
@misc{reference.wolfram_2025_matrixnormaldistribution, author="Wolfram Research", title="{MatrixNormalDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixNormalDistribution.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_matrixnormaldistribution, organization={Wolfram Research}, title={MatrixNormalDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/MatrixNormalDistribution.html}, note=[Accessed: 03-March-2026]}