InverseWishartMatrixDistribution
InverseWishartMatrixDistribution[ν,Σ]
自由度 ν,共分散行列 Σ の逆Wishart 行列分布を表す.
詳細
- 逆Wishart行列分布における対称行列
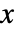 の確率密度は
の確率密度は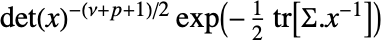 に比例する.ただし,
に比例する.ただし,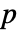 は行列 Σ の大きさである.
は行列 Σ の大きさである. - InverseWishartMatrixDistribution[ν,Σ]として分布している行列
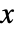 について,逆行列
について,逆行列 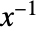 はWishartMatrixDistribution[ν,Σ-1]として分布する.
はWishartMatrixDistribution[ν,Σ-1]として分布する. - 共分散行列
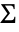 は次元が
は次元が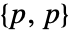 の正定値対称行列でよく,ν は
の正定値対称行列でよく,ν は 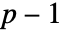 より大きい任意の実数でよい.
より大きい任意の実数でよい. - InverseWishartMatrixDistributionは,MatrixPropertyDistribution,EstimatedDistribution,RandomVariate等の関数とともに使うことができる.
例題
すべて開くすべて閉じる例 (3)
スコープ (6)
両分布のLogLikelihoodを比較する:
特性と関係 (3)
![]() (
(![]() および
および ![]() は独立ガウス(Gauss)ベクトルおよびWishart行列)はHotellingTSquareDistributionに従う:
は独立ガウス(Gauss)ベクトルおよびWishart行列)はHotellingTSquareDistributionに従う:
MatrixPropertyDistributionを使って式 ![]() をサンプルする:
をサンプルする:
テキスト
Wolfram Research (2015), InverseWishartMatrixDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html (2017年に更新).
CMS
Wolfram Language. 2015. "InverseWishartMatrixDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html.
APA
Wolfram Language. (2015). InverseWishartMatrixDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseWishartMatrixDistribution.html