JacobiAmplitude[u,m]
gives the amplitude ![]() for Jacobi elliptic functions.
for Jacobi elliptic functions.




JacobiAmplitude
JacobiAmplitude[u,m]
gives the amplitude ![]() for Jacobi elliptic functions.
for Jacobi elliptic functions.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- JacobiAmplitude[u,m] converts from the argument u for an elliptic function to the amplitude ϕ.
- JacobiAmplitude is the inverse of the elliptic integral of the first kind. If
![u=TemplateBox[{phi, m}, EllipticF] u=TemplateBox[{phi, m}, EllipticF]](Files/JacobiAmplitude.en/2.png) , then
, then ![phi=TemplateBox[{u, m}, JacobiAmplitude] phi=TemplateBox[{u, m}, JacobiAmplitude]](Files/JacobiAmplitude.en/3.png) .
. - JacobiAmplitude[u,m] has a branch cut discontinuity in the complex u plane running from
![2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+1) TemplateBox[{{1, -, m}}, EllipticK] 2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+1) TemplateBox[{{1, -, m}}, EllipticK]](Files/JacobiAmplitude.en/4.png) to
to ![2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+3) TemplateBox[{{1, -, m}}, EllipticK] 2 s TemplateBox[{m}, EllipticK]+ⅈ (4 t+3) TemplateBox[{{1, -, m}}, EllipticK]](Files/JacobiAmplitude.en/5.png) for every pair of integers
for every pair of integers 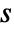 and
and 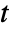 .
. - For certain special arguments, JacobiAmplitude automatically evaluates to exact values.
- JacobiAmplitude can be evaluated to arbitrary numerical precision.
- JacobiAmplitude automatically threads over lists.
Examples
open all close allBasic Examples (4)
Scope (26)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments:
Evaluate JacobiAmplitude efficiently at high precision:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix JacobiAmplitude function using MatrixFunction:
Specific Values (4)
Visualization (3)
Plot the JacobiAmplitude functions for various values of parameter ![]() :
:
Plot JacobiAmplitude as a function of its parameter ![]() :
:
Function Properties (5)
It has no singularities or discontinuities:
JacobiAmplitude is neither non-negative nor non-positive:
JacobiAmplitude is neither convex nor concave:
Differentiation (3)
Series Expansions (3)
Plot the first three approximations for ![]() around
around ![]() :
:
Plot the first three approximations for ![]() around
around ![]() :
:
JacobiAmplitude can be applied to a power series:
Function Representations (3)
Applications (4)
Solution of the pendulum equation in the overswing mode:
Check with the pendulum equation:
Relativistic solution of the sine‐Gordon equation:
Verify the solution by substituting into the sine‐Gordon equation:
Plot the solution for different values of ![]() and
and ![]() :
:
Form and plot generalized Fourier series:
Spherical triangle from an elliptic parameter ![]() and triple
and triple ![]() such that
such that ![]() :
:
Angles at vertices ![]() ,
, ![]() and
and ![]() and sides opposite to each corresponding vertex:
and sides opposite to each corresponding vertex:
Verify Cagnoli's equation, which relates the measurements of all the angles and sides of a spherical triangle:
Compute the area of the triangle, also known as the spherical excess:
Compute the excess using L'Huilier's theorem [MathWorld]:
Compute corresponding points on 3D unit sphere:
Properties & Relations (5)
Compose with inverse functions:
Use PowerExpand to disregard the multivaluedness of the inverse function:
Apply trigonometric functions to JacobiAmplitude:
Solve a transcendental equation:
Obtain from a differential equation:
JacobiAmplitude has branch cuts from ![]() to
to ![]() for any integers
for any integers ![]() and
and ![]() :
:
Tech Notes
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 2020 (12.1)
Text
Wolfram Research (1988), JacobiAmplitude, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiAmplitude.html (updated 2020).
CMS
Wolfram Language. 1988. "JacobiAmplitude." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/JacobiAmplitude.html.
APA
Wolfram Language. (1988). JacobiAmplitude. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiAmplitude.html
BibTeX
@misc{reference.wolfram_2025_jacobiamplitude, author="Wolfram Research", title="{JacobiAmplitude}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/JacobiAmplitude.html}", note=[Accessed: 28-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_jacobiamplitude, organization={Wolfram Research}, title={JacobiAmplitude}, year={2020}, url={https://reference.wolfram.com/language/ref/JacobiAmplitude.html}, note=[Accessed: 28-February-2026]}