JacobiSymbol
JacobiSymbol[n,m]
给出雅可比(Jacobi)符号 ![]() .
.
更多信息
- 整数型数学函数,同时适合符号和数值运算.
- 对素数 m,Jacobi 符号简化为勒让德(Legendre)符号. 勒让德符号等于
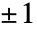 取决于 n 是否是一个模 m 的二次剩余.
取决于 n 是否是一个模 m 的二次剩余. - JacobiSymbol 自动逐项作用于列表.
范例
打开所有单元关闭所有单元
Wolfram Research (1988),JacobiSymbol,Wolfram 语言函数,https://reference.wolfram.com/language/ref/JacobiSymbol.html.
文本
Wolfram Research (1988),JacobiSymbol,Wolfram 语言函数,https://reference.wolfram.com/language/ref/JacobiSymbol.html.
CMS
Wolfram 语言. 1988. "JacobiSymbol." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/JacobiSymbol.html.
APA
Wolfram 语言. (1988). JacobiSymbol. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/JacobiSymbol.html 年